Ultimo aggiornamento: 30 Oct. 2024

Calcolatore della Frequenza di Risonanza

Q: Che cos'è la frequenza di risonanza?

La frequenza di risonanza è la frequenza naturale e non smorzata di un sistema. Se applichiamo una frequenza di risonanza, le oscillazioni prendono la massima ampiezza e anche se la forza in questione è relativamente piccola, può produrre grandi ampiezze . Tuttavia, se si sceglie un'altra frequenza, il segnale viene smorzato .

Q: Come si calcola la frequenza di risonanza di un circuito LC?

Per calcolare la frequenza di risonanza di un circuito composto da un induttore e un condensatore, segui questi passaggi: Scrivi la capacità C in farad; Scrivi l' induttanza L in henry; e Inserisci entrambi i parametri nella formula della frequenza di risonanza : f = 1 / (2π × √(L × C)) .

Q: Qual è la frequenza di risonanza se C=220 pF e L=1 mH?

339,32 kHz . In un circuito LC la cui capacità è di 220 pF = 2,20 × 10 -10 F e l'induttanza è di 1 mH = 0,001 H , la frequenza di risonanza è: f = 1 / (2π × √(2,20 × 10 -10 × 0,001)) = 339 319 Hz ≈ 339,32 kHz .

Creato da Dott. Hanna Pamuła, Ph.D.

Revisione eseguita da Bogna Szyk e Jack Bowater

Tradotto da Agata Flak

Agata Flak

Linguistic freak at first sight, but VERY curious about numbers. Back in high school, she most enjoyed the satisfaction of getting the perfect result in a maths exercise or discovering something (not necessarily revolutionary) during a year-long project about cucumber hydrolysis. She can stay up far into the night, googling how much water there is in 400 ml of soup or how many ants it would take to make a car collapse under their weight. Weird, but oddly specific, and always highly meticulous. See full profile

Check our editorial policy

e Rangsimatiti Binda Saichompoo

Rangsimatiti Binda Saichompoo

With an environmental mind, Kat is currently pursuing a Master’s degree in Biomass Engineering and Bioeconomy. Kat joined Omni as an Italian and French translator. Apart from translating, writing content, and sometimes creating calculators, she loves nature, reading, sports, and playing lots of board games. See full profile

Check our editorial policy

Nuovo

Indice

Che cos'è un circuito LC (circuito oscillante)?Che cos'è la frequenza di risonanza?Come si calcola la frequenza di risonanza di un circuito LC?Come si utilizza il calcolatore della frequenza di risonanza?FAQ

Se vuoi calcolare la frequenza di risonanza di un circuito LC, non cercare oltre — questo calcolatore della frequenza di risonanza è lo strumento che fa per te. Inserisci l'induttanza e la capacità, e in un attimo troverai la frequenza di risonanza e quella angolare. Ti forniamo anche un po' di teoria che ti può tornare utile — di seguito scoprirai come calcolare la frequenza di risonanza e una breve definizione su cosa sia effettivamente la frequenza di risonanza.

Se ti interessano i circuiti elettronici, probabilmente vorrai sapere come ottenere una frazione del voltaggio in ingresso. Il nostro calcolatore per il partitore di tensione 🇺🇸 è quello che ti serve.

Che cos'è un circuito LC (circuito oscillante)?

Un circuito LC (chiamato anche circuito oscillante) è un circuito risonante idealizzato a resistenza zero. Se stai cercando un circuito "non ideale", vai al nostro calcolatore per il circuito RLC 🇺🇸!

Un circuito LC contiene solo un induttore e un condensatore, in parallelo o in serie:

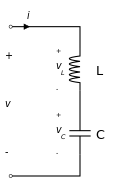
I circuiti oscillati sono comunemente utilizzati come generatori di segnale e filtri passabanda. Infatti, essi selezionano un segnale a una particolare frequenza da un segnale più complesso. Peraltro, sono ampiamente utilizzati in elettronica — puoi trovare circuiti LC in amplificatori, oscillatori, sintonizzatori, trasmettitori e ricevitori radio. I circuiti LC e RC possono essere utilizzati per filtrare un segnale bloccando determinate frequenze.

🙋 Omni dispone di altri ottimi strumenti per aiutarti nei tuoi studi di elettronica. Prova il nostro calcolatore per il circuito RC 🇺🇸 o la nostra collezione di strumenti per circuiti semplici:

Che cos'è la frequenza di risonanza?

La frequenza di risonanza è la frequenza naturale e non smorzata di un sistema. Se applichiamo una frequenza di risonanza, le oscillazioni prendono la massima ampiezza e anche se la forza in questione è relativamente piccola, può produrre grandi ampiezze. Tuttavia, se si sceglie un'altra frequenza, il segnale viene smorzato.

Esistono diversi tipi di risonanze, ad esempio:

Meccanica e acustica;
Elettrica;
Ottica;
Orbitale; e
Molecolare.

Per i circuiti LC, la frequenza di risonanza è determinata dalla capacità C e dall'impedenza L.

Come si calcola la frequenza di risonanza di un circuito LC?

Per calcolare la frequenza di risonanza di un circuito composto da un induttore e un condensatore, segui questi passaggi:

Scrivi la capacità C in farad;
Scrivi l'induttanza L in henry; e
Inserisci entrambi i parametri nella formula della frequenza di risonanza: f = 1 / (2π × √(L × C)).

In questa formula:

$f$ — Frequenza di risonanza;
$L$ — Induttanza del circuito; e
$C$ — Capacità del circuito.

Da dove deriva questa formula? La risonanza nel circuito LC compare quando la reattanza induttiva dell'induttore diventa uguale alla reattanza capacitiva del condensatore. Quindi:

xL = 2\pi\times f\times L

xC = \frac{1}{2\pi\times f\times C}

Dopo aver trasformato l'equazione, troviamo:

\begin{split} xL&=xC\\ 2\pi\times f\times L&=\frac{1}{2\pi\times f\times C} \end{split}

Dunque:

f^2 = \frac{1}{4\pi^2\times L \times C}

E infine:

f = \frac{1}{2\pi\sqrt{L\times C}}

Inoltre, la frequenza angolare può essere calcolata in base alla seguente e ben nota formula:

\omega = 2\times \pi \times f

Come si utilizza il calcolatore della frequenza di risonanza?

Utilizzare il nostro strumento è una passeggiata:

Inserisci il valore del condensatore. Ad esempio, la nostra capacità è pari a $1\ \mathrm{μF}$ ;
Inserisci l'induttanza. L'induttanza del nostro circuito LC è pari a $0,\!18\ \mathrm{mH}$ ; e
Il calcolatore della frequenza di risonanza ha fatto il suo lavoro! Abbiamo scoperto rapidamente qual è la frequenza di risonanza: $11,\!863\ \mathrm{kHz}$ . Puoi anche controllare la frequenza angolare: questo valore apparirà sotto la frequenza di rizonanza.

Il calcolatore della frequenza di risonanza è uno strumento flessibile, quindi — come al solito — puoi digitare due variabili qualsiasi e quella mancante verrà calcolata in un attimo.

FAQ

Qual è la frequenza di risonanza se C=220 pF e L=1 mH?

339,32 kHz. In un circuito LC la cui capacità è di 220 pF = 2,20 × 10^-10 F e l'induttanza è di 1 mH = 0,001 H, la frequenza di risonanza è: f = 1 / (2π × √(2,20 × 10^-10 × 0,001)) = 339 319 Hz ≈ 339,32 kHz.

In che modo le radio utilizzano la frequenza di risonanza?

Quando selezioni una stazione radio specifica, stai sintonizzando la frequenza di risonanza del circuito LC all'interno della radio in modo che corrisponda alla frequenza del segnale in entrata, filtrando tutti gli altri segnali.