Ultimo aggiornamento: 30 Oct. 2024

Calcolatore per il Volume del Serbatoio

Q: Come si calcola il volume di un serbatoio?

Puoi provare a utilizzare il calcolatore per il volume del serbatoio di Omni Calculator, oppure procedere come segue: Ottieni il raggio interno e l' altezza del serbatoio ; Eleva al quadrato il raggio, quindi moltiplicalo per pi greco (3,14159...). Congratulazioni, hai ottenuto l' area della base del serbatoio; quindi Moltiplica il risultato per l'altezza e otterrai il volume del serbatoio .

Q: Come calcolare la capacità del mio motore?

Gli esperti di auto la chiamano cilindrata, e puoi calcolarla come segue: Ottieni il volume di uno dei cilindri del tuo motore. Puoi provare il calcolatore per il volume del serbatoio di Omni Calculator, o determinare il raggio e l'altezza del cilindro (corsa del pistone) per fare i calcoli a mano; Eleva al quadrato il raggio, moltiplicalo per pi greco (3,14159...), e poi per la corsa del pistone; e infine Moltiplica il volume del cilindro per il numero di cilindri nel tuo motore e otterrai la capacità del motore.

Q: Per quanto tempo si può tenere l'acqua in un serbatoio?

Dipende dalla quantità di acqua e dalla velocità di deflusso. Per calcolare il tempo, procedi come segue: Calcola il volume del tuo serbatoio con il calcolatore per il volume del serbatoio di Omni Calculator. Assicurati di avere il valore in litri; Determina quanti litri consumi al giorno ; quindi Dividi la quantità di acqua che hai per il tuo consumo giornaliero. Il risultato è il numero di giorni prima che l'acqua finisca.

Q: Perché i serbatoi cilindrici sono più usati dei serbatoi rettangolari?

Ci sono due ragioni principali per cui preferiamo i serbatoi cilindrici a quelli rettangolari: I serbatoi cilindrici resistono meglio alla pressione rispetto a quelli rettangolari. Di conseguenza, i produttori hanno bisogno di meno materiale per costruirli; e I serbatoi rettangolari sono più difficili da pulire , nello specifico negli angoli.

Q: Qual è il volume di un barile di petrolio?

218,7 L . Un barile di petrolio ha un diametro di 0,572 m e un'altezza di 0,851 m. Inserisci queste cifre nella seguente formula: Volume = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 litri .

Creato da Dott. Hanna Pamuła, Ph.D.

Revisione eseguita da Bogna Szyk e Jack Bowater

Tradotto da Agata Flak

Agata Flak

Linguistic freak at first sight, but VERY curious about numbers. Back in high school, she most enjoyed the satisfaction of getting the perfect result in a maths exercise or discovering something (not necessarily revolutionary) during a year-long project about cucumber hydrolysis. She can stay up far into the night, googling how much water there is in 400 ml of soup or how many ants it would take to make a car collapse under their weight. Weird, but oddly specific, and always highly meticulous. See full profile

Check our editorial policy

e Rangsimatiti Binda Saichompoo

Rangsimatiti Binda Saichompoo

With an environmental mind, Kat is currently pursuing a Master’s degree in Biomass Engineering and Bioeconomy. Kat joined Omni as an Italian and French translator. Apart from translating, writing content, and sometimes creating calculators, she loves nature, reading, sports, and playing lots of board games. See full profile

Check our editorial policy

Nuovo

Indice

Come utilizzare il calcolatore per il volume del serbatoio?Formula del volume del serbatoio cilindrico Calcolatore per il volume del serbatoio rettangolare (prisma rettangolare)Formula del volume di una capsula Volume del serbatoio ellittico (serbatoio ovale)Volume del tronco di cono — Serbatoio a tronco di cono Volume del serbatoio a fondo conico e serbatoi con parte superiore conica FAQ

Con questo calcolatore per il volume del serbatoio puoi stimare facilmente il volume del tuo serbatoio o di qualunque contenitore. Scegli tra dieci diverse forme di serbatoio, dai serbatoi rettangolari e cilindrici ai serbatoi a capsula ed ellittici. Puoi anche trovare il volume di un tronco di cono nei serbatoi a fondo conico. Basta inserire le dimensioni del tuo contenitore e questo strumento calcolerà per te il volume totale del serbatoio. Puoi anche indicare l'altezza di riempimento, che verrà utilizzata per trovare il volume di riempimento.

Ti chiedi come funziona questo calcolatore? Continua a leggere e troverai tutte le formule di cui hai bisogno — il volume di un serbatoio a capsula, di un serbatoio ellittico o dei diffusissimi serbatoi a fondo conico (talvolta chiamati serbatoi conici), oltre a molte altre!

Stai cercando altri tipi di serbatoi e contenitori di forme diverse e per altre applicazioni? Dai un'occhiata al nostro calcolatore di volume per trovare il volume dei più comuni solidi tridimensionali. Per qualcosa di più specialistico, puoi anche dare un'occhiata al calcolatore per acquari e al calcolatore per il volume della piscina per trovare soluzioni ai problemi di volume di tutti i giorni.

Come utilizzare il calcolatore per il volume del serbatoio?

Questo calcolatore per il volume del serbatoio è un semplice strumento che ti aiuta a trovare il volume di un serbatoio o contenitore, e il volume di riempimento. Puoi scegliere tra dieci forme di serbatoio:

Cilindro verticale;
Cilindro orizzontale;
Prisma rettangolare (scatola);
Capsula verticale;
Capsula orizzontale;
Ovale verticale (ellittico);
Ovale orizzontale (ellittico);
Fondo conico;
Parte superiore conica; e
Tronco di cono (a forma di imbuto).

"Ma come si usa questo calcolatore per il volume del serbatoio?", ti starai chiedendo. Vediamo un semplice esempio:

Decidi la forma. Supponiamo di voler trovare il volume di un serbatoio cilindrico verticale. Scegli questa opzione dall'elenco a tendina. L'immagine schematica del serbatoio apparirà sotto il calcolatore; assicurati che sia quella desiderata!
Inserisci le dimensioni del serbatoio. Nel nostro caso, dobbiamo riempire i campi Altezza e Diametro. Nel nostro esempio, questi sono pari a $32\ \mathrm{cm}$ e $24\ \mathrm{cm}$ , rispettivamente. Inoltre, possiamo inserire l'altezza di riempimento — $28\ \mathrm{cm}$ ; e
Il calcolatore per il volume del serbatoio ha già trovato il volume totale e il volume di riempimento! Il volume totale del serbatoio è $14,\!48\ \mathrm{L}$ , mentre il volume del liquido all'interno è $12,\!67 \ \mathrm{L}$ . Come sempre, puoi cambiare le unità di misura cliccando sulle unità di misura del volume. Facile!

Formula del volume del serbatoio cilindrico

Per calcolare il volume totale di un serbatoio cilindrico, o qualunque tipo di contenitore cilindrico, tutto ciò che dobbiamo sapere è il diametro del cilindro (o raggio) e l'altezza del cilindro (che può essere chiamata lunghezza se si trova in posizione orizzontale).

Serbatoio cilindrico verticale

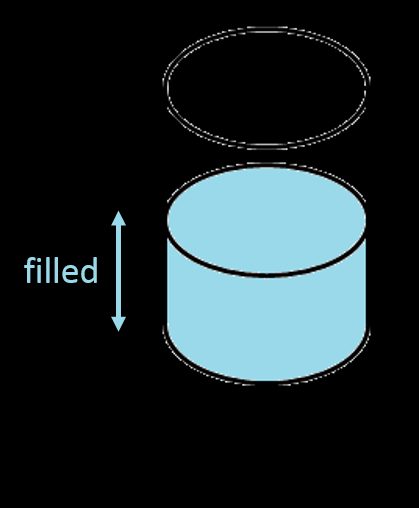
Possiamo trovare il volume totale di un serbatoio cilindrico con la formula standard del volume — l'area della base moltiplicata per l'altezza. Un cerchio è la forma della base, quindi la sua area, secondo la nota equazione, è uguale a $\pi \times \mathrm{raggio}^2$ . Pertanto la formula per il volume di un serbatoio cilindrico verticale è la seguente:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ verticale}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h \end{split}

dove:

$r$ — Raggio della base; e
$h$ — Altezza del cilindro.

Se vogliamo calcolare il volume di riempimento, dobbiamo trovare il volume di un cilindro "più corto". È molto semplice!

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ verticale}}} &= \pi \times r^2 \times f\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times f \end{split}

dove:

$f$ — Altezza fino a dove sarà riempito il cilindro.

Serbatoio cilindrico orizzontale

Il volume totale di un serbatoio cilindrico orizzontale può essere trovato in modo analogo — è l'area dell'estremità circolare moltiplicata per la lunghezza del cilindro:

\begin{split} V_{\scriptsize{\mathrm{\tiny cilindro\ orizzontale}}} &= \pi \times r^2 \times l\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times l \end{split}

dove:

$l$ — Lunghezza del cilindro.

Sezione trasversale di un serbatoio cilindrico parzialmente riempito in parte.

Le cose si complicano quando vogliamo trovare il volume del cilindro orizzontale parzialmente riempito. Per prima cosa, dobbiamo trovare l'area della base — l'area del segmento circolare coperta dal liquido:

A_{\mathrm{\tiny segmento}} = \frac{1}{2}\times r^2 \times (\theta-\sin(\theta))

dove:

$r$ — Raggio della base; e
$\theta$ — Angolo centrale del segmento.

L'angolo $\theta$ può essere ricavato dalla formula del coseno:

\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f}

dove:

$f$ — Altezza fino a dove è riempito il cilindro orizzontale.

Quindi:

\theta= 2\times \arccos\left(\frac{r-f}{f}\right)

Infine, la formula del volume di un cilindro orizzontale parzialmente riempito $V_{\scriptsize{\mathrm{C_{pr}}}}$ è:

\small V_{\scriptsize{\mathrm{C_{pr}}}} = 0,\!5\times r^2\times(\theta -\sin(\theta))\times l

dove:

\theta = 2\times \arccos\left(\frac{r-f}{r}\right)

Se il serbatoio o contenitore è pieno per più di metà, allora è più facile sottrarre la parte vuota dal volume totale.

Calcolatore per il volume del serbatoio rettangolare (prisma rettangolare)

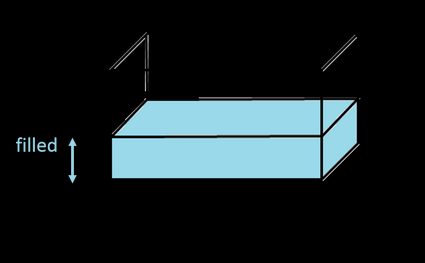
Se ti stai chiedendo come calcolare il volume di un serbatoio o contenitore rettangolare (noto anche come cuboide, scatola o esaedro rettangolare), non cercare oltre! Questo tipo di contenitore è spesso chiamato serbatoio rettangolare, ma questo non è il suo nome corretto, perché un rettangolo è una forma bidimensionale, quindi non ha un volume.

Per trovare il volume del prisma rettangolare, moltiplica tutte le dimensioni del serbatoio:

V_{{\mathrm{prisma\ rettangolare}}} = h\times w\times l

dove:

$h$ — Altezza del serbatoio;
$w$ — Larghezza del serbatoio; e
$l$ — Lunghezza del serbatoio.

Se vuoi sapere qual è il volume del liquido in questo serbatoio, inserisci l'altezza di riempimento al posto dell'altezza del contenitore. Il volume di un prisma rettangolare parzialmente riempito, $V_{\scriptsize{\mathrm{R_{pr}}}}$ , è:

V_{{\mathrm{R_{pr}}}} = f\times w\times l

dove:

$f$ — Altezza fino a dove è riempito il prisma rettangolare.

Per questo calcolatore per il volume del serbatoio, non importa che il serbatoio sia in posizione orizzontale o verticale. Assicurati solo che il Riempimento e l'Altezza siano sullo stesso asse.

Formula del volume di una capsula

Il nostro strumento definisce una capsula come due semisfere separate da un cilindro. Per calcolare il volume totale di una capsula, basta sommare il volume della sfera a quello del cilindro:

V_{\scriptsize{\mathrm{capsula}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!l\right)

A seconda della posizione del serbatoio, il calcolatore per il volume del serbatoio utilizzerà una formula leggermente diversa:

1. Serbatoio a capsula orizzontale parzialmente riempito

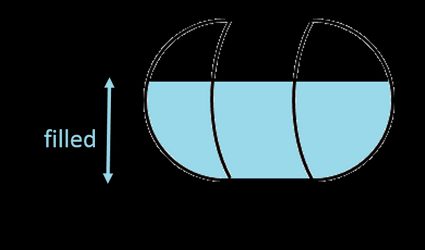
Serbatoio a capsula orizzontale con dimensioni.

Poiché le semisfere alle due estremità del serbatoio sono identiche, formano una sfera intera, addiziona il volume della sfera, $V_{\scriptsize{\mathrm{sfera}}}$ al cilindro orizzontale $V_{\scriptsize{\mathrm{cilindro\ orizzontale}}}$ (dai un'occhiata al paragrafo precedente) per calcolare il volume del liquido in una capsula orizzontale riempita ( $V_{\scriptsize{\mathrm{capsula}}}$ ):

\begin{split} &V_{\scriptsize{\mathrm{capsula}}} = V_{\scriptsize{\mathrm{sfera}}}+V_{\scriptsize{\mathrm{cilindro\ orizzontale}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times l \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right) \end{split}

dove:

$d$ — Diametro del serbatoio;
$f$ — Altezza di riempimento; e
$\theta$ — Angolo corrispondente al settore riempito del serbatoio.

2. Serbatoio a capsula verticale parzialmente riempito

La formula varia in base alle diverse altezze di riempimento. In tutte le formule successive, incontreremo queste quantità:

$d$ — Diametro del serbatoio;
$f$ — Altezza di riempimento; e
$l$ — Lunghezza della parte cilindrica.

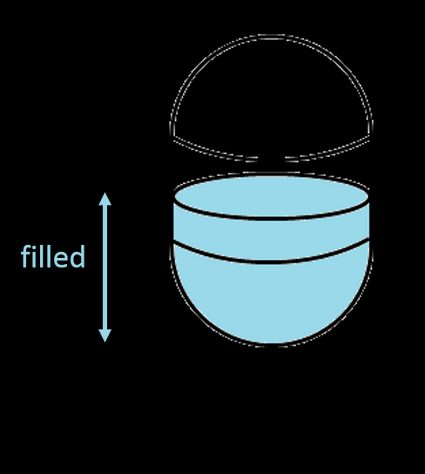
Serbatoio a capsula verticale con dimensioni.

Se $f < d/2$ , allora il liquido si trova solo nella parte inferiore della semisfera, quindi ci serve solo la formula del volume di una sfera:

V_{\scriptsize{\mathrm{capsula}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right)

Se $d/2 < f < d/2 +l$ , allora dobbiamo sommare il volume della semisfera a quello del cilindro "più corto":

\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{capsula}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}

Se $d/2 + l < f$ , significa che la semisfera inferiore e il cilindro sono pieni, quindi dobbiamo solo sottrarre la semisfera superiore dall'intero volume:

\begin{split} &V_{\scriptsize{\mathrm{capsula}}} = V_{\scriptsize{\mathrm{totale\ capsula}}}\! -\! \frac{\pi\times(l+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (l+d-f)\right) \end{split}

Volume del serbatoio ellittico (serbatoio ovale)

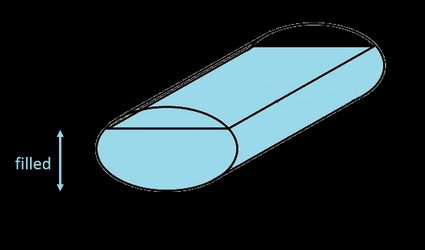
Serbatoio ovale orizzontale con dimensioni.

Nel nostro calcolatore, definiamo un serbatoio ovale come un serbatoio cilindrico con un'estremità ellittica. Per trovare il volume totale di un serbatoio ellittico, devi moltiplicare l'area dell'ellissi per la lunghezza del serbatoio:

V_{\scriptsize{\mathrm{elissi}}} = \pi\!\times\!w\!\times\!l\!\times\!\frac{h}{4}

dove:

$w$ — Larghezza del serbatoio;
$h$ — Altezza del serbatoio; e
$l$ — Lunghezza del serbatoio.

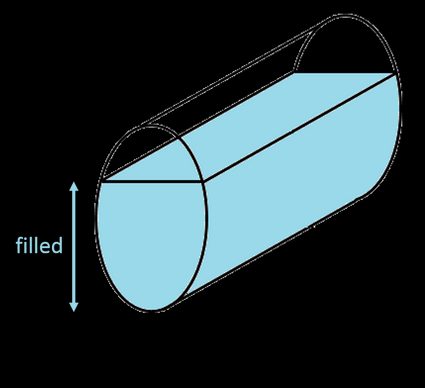
Serbatoio ovale verticale con dimensioni.

Finalmente un'altra formula facile! Purtroppo, trovare il volume di un serbatoio parzialmente riempito, sia in posizione orizzontale che verticale, non è così semplice. Devi utilizzare la formula dell'area del segmento dell'ellisse e moltiplicare il risultato per la lunghezza del serbatoio:

\begin{split} &V_{\scriptsize{\mathrm{elissi\ riempita}}} = l\!\times\!h\!\times\!\frac{w}{4}\\[1em] &\qquad\times\!\left[\arccos\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Volume del tronco di cono — Serbatoio a tronco di cono

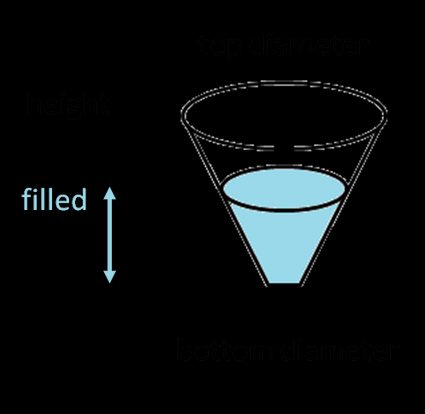
Serbatoio a tronco di cono con dimensioni.

Per calcolare il volume del tronco di cono (una forma particolare che abbiamo incontrato nel nostro calcolatore per il tronco di cono 🇺🇸), usa la formula:

\begin{split} &V_{\scriptsize{\mathrm{tronco}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cono}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\!+\! \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

dove:

$d_{\mathrm{sup}}$ — Diametro superiore del tronco di cono;
$d_{\mathrm{inf}}$ — Diametro inferiore del tronco di cono; e
$h_{\mathrm{cono}}$ — Altezza del serbatoio.

Serbatoio a tronco di cono con dimensioni e altezza di riempimento.

Se vuoi trovare il volume del tronco di cono parzialmente riempito per una determinata altezza di riempimento, calcola prima il raggio superiore della parte riempita:

R = \frac{1}{2} \times d_{\mathrm{sup}}\times \frac{f+z}{h_{\mathrm{cono}}+z}

dove:

z = h_\mathrm{cono} \times \frac{d_{\mathrm{inf}}}{d_{\mathrm{sup}}-d_{\mathrm{inf}}}

(Puoi ricavare la formula dalla similitudine dei triangoli.)

In seguito, basta trovare il nuovo volume del tronco di cono:

\begin{split} &V_{\scriptsize{\mathrm{tronco\ riempito}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{inf}}}{2} + \left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

Volume del serbatoio a fondo conico e serbatoi con parte superiore conica

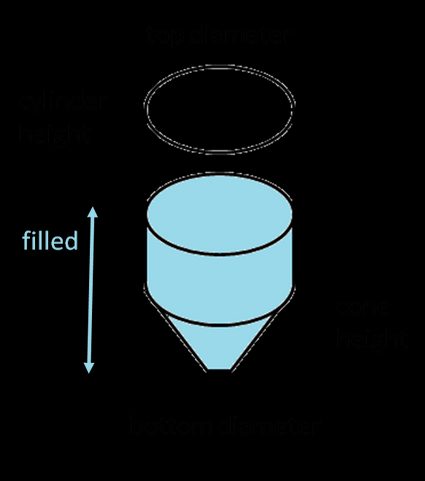
Serbatoio a fondo conico con dimensioni.

Trovare il volume totale di un serbatoio a fondo conico non è così difficile — basta aggiungere il volume della parte a tronco di cono al volume della parte cilindrica:

\begin{split} &{V_{\scriptsize{\mathrm{fondo\ conico}}} = V_{\scriptsize{\mathrm{tronco}}} + V_{\scriptsize{\mathrm{cilindro}}}}\\[1em] & {=\frac{1}{3}\times\pi\times h_{\mathrm{cono}} \times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\right.}\\[1.4em] &{\qquad \left.+ \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right)}\\[1.4em] &{\qquad+\pi\times\left(\frac{d_{\mathrm{sup}}}{2}\right)^2\times h_{\mathrm{cilindro}}} \end{split}

dove:

$d_{\mathrm{sup}}$ — Diametro superiore del tronco di cono;
$d_{\mathrm{inf}}$ — Diametro inferiore del tronco di cono;
$h_{\mathrm{cono}}$ — Altezza della parte conica del serbatoio; e
$h_{\mathrm{cilindro}}$ — Altezza della parte cilindrica del serbatoio.

Per calcolare il volume di riempimento, basta sommare il volume del fondo conico alla parte cilindrica, a seconda del livello del liquido, utilizzando le equazioni precedenti.

Il calcolo del volume totale del serbatoio con parte superiore conica è esattamente lo stesso del serbatoio a fondo conico. L'unica differenza è quando si vuole trovare la parte riempita — ovviamente, prima si riempie la parte cilindrica, e solo dopo il tronco di cono.

🙋 Hai calcolato tutti i tuoi volumi utilizzando le unità metriche, ma hai bisogno di quelle imperiali? Non preoccuparti, perché Omni ha una soluzione pratica per tutte le tue esigenze — usa il nostro convertitore di volume 🇺🇸 per convertire rapidamente le unità di volume!

FAQ

Come si calcola il volume di un serbatoio?

Puoi provare a utilizzare il calcolatore per il volume del serbatoio di Omni Calculator, oppure procedere come segue:

Ottieni il raggio interno e l'altezza del serbatoio;
Eleva al quadrato il raggio, quindi moltiplicalo per pi greco (3,14159...). Congratulazioni, hai ottenuto l'area della base del serbatoio; quindi
Moltiplica il risultato per l'altezza e otterrai il volume del serbatoio.

Come calcolare la capacità del mio motore?

Gli esperti di auto la chiamano cilindrata, e puoi calcolarla come segue:

Ottieni il volume di uno dei cilindri del tuo motore. Puoi provare il calcolatore per il volume del serbatoio di Omni Calculator, o determinare il raggio e l'altezza del cilindro (corsa del pistone) per fare i calcoli a mano;
Eleva al quadrato il raggio, moltiplicalo per pi greco (3,14159...), e poi per la corsa del pistone; e infine
Moltiplica il volume del cilindro per il numero di cilindri nel tuo motore e otterrai la capacità del motore.

Per quanto tempo si può tenere l'acqua in un serbatoio?

Dipende dalla quantità di acqua e dalla velocità di deflusso. Per calcolare il tempo, procedi come segue:

Calcola il volume del tuo serbatoio con il calcolatore per il volume del serbatoio di Omni Calculator. Assicurati di avere il valore in litri;
Determina quanti litri consumi al giorno; quindi
Dividi la quantità di acqua che hai per il tuo consumo giornaliero. Il risultato è il numero di giorni prima che l'acqua finisca.

Perché i serbatoi cilindrici sono più usati dei serbatoi rettangolari?

Ci sono due ragioni principali per cui preferiamo i serbatoi cilindrici a quelli rettangolari:

I serbatoi cilindrici resistono meglio alla pressione rispetto a quelli rettangolari. Di conseguenza, i produttori hanno bisogno di meno materiale per costruirli; e
I serbatoi rettangolari sono più difficili da pulire, nello specifico negli angoli.

Qual è il volume di un barile di petrolio?

218,7 L. Un barile di petrolio ha un diametro di 0,572 m e un'altezza di 0,851 m. Inserisci queste cifre nella seguente formula:

Volume = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,2187 m² = 218,7 litri.