Calcolatore per la Deflessione delle Travi
Questo calcolatore per la deflessione delle travi ti aiuterà a determinare la deflessione massima di travi a semplice sostegno e a sbalzo che trasportano configurazioni di carico semplici.
Puoi scegliere tra una selezione di tipi di carico che possono agire su qualsiasi lunghezza di trave. L'entità e la posizione di questi carichi influenzano la flessione della trave.
In questo calcolatore per la deflessione delle travi, imparerai a conoscere le diverse formule di deflessione delle travi utilizzate per calcolare le deflessioni delle travi semplicemente supportate e le deflessioni delle travi a sbalzo. Scoprirai anche come il modulo di elasticità della trave e il suo momento d'inerzia dell'area trasversale influiscono sulla deflessione massima calcolata della trave.
La deflessione della trave è una parte importante dell'analisi delle travi, ma un'altra parte importante è l'analisi delle sollecitazioni. Il modulo di sezione è un potente strumento per studiare le sollecitazioni di flessione della trave, che puoi calcolare utilizzando il nostro calcolatore del modulo di resistenza 🇺🇸.
Cosa sono la deflessione e la flessione della trave?

Nell'edilizia, di solito si utilizzano strutture portanti che vengono tenute in posizione dalle fondamenta nel terreno. Queste strutture sono come lo scheletro di edifici, case e persino ponti. In un'intelaiatura, le strutture verticali sono chiamate pilastri e quelle orizzontali travi. Le travi sono i membri estesi di una struttura che trasportano i carichi portati dai solai orizzontali delle strutture come i pavimenti in cemento armato, i sistemi di travetti in legno e i tetti.
Quando le travi trasportano carichi troppo pesanti per loro, iniziano a piegarsi. La flessione della trave si chiama deflessione della trave. La deflessione della trave è lo spostamento verticale di un punto lungo il centro di una trave. Possiamo anche considerare la superficie della trave come punto di riferimento, a patto che non ci siano cambiamenti nell'altezza o nella profondità della trave durante la flessione.
Come si calcola la massima deflessione della trave?
Abbiamo dotato il nostro calcolatore per la deflessione delle travi delle formule che ingegneri e studenti di ingegneria utilizzano per determinare rapidamente la deflessione massima che una specifica trave subirà a causa del carico che trasporta. Tuttavia, queste formule possono risolvere solo carichi semplici e una combinazione di questi carichi. Abbiamo tabulato queste formule per te, come mostrato di seguito:
Formule di deflessione delle travi a semplice appoggio
Trave e carico | Formula della deflessione massima della trave () |
|---|---|
 | |
 | |
 | |
 | |
 | |
 |
Formule di deflessione delle travi a mensola
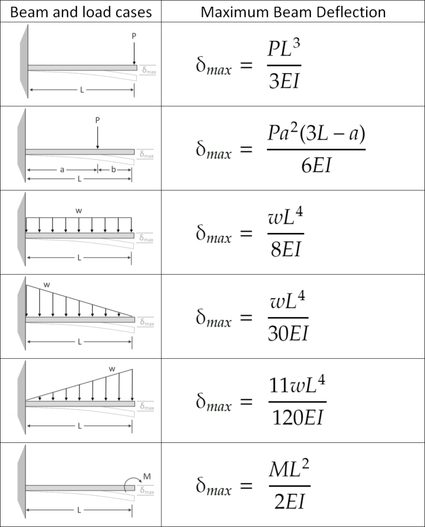
Metodo della sovrapposizione
Per calcolare la deflessione massima di una trave con una combinazione di carichi, possiamo utilizzare il metodo della sovrapposizione. Il metodo della sovrapposizione stabilisce che possiamo approssimare la deflessione totale di una trave sommando tutte le deflessioni provocate da ogni configurazione di carico. Tuttavia, questo metodo ci fornisce solo un valore approssimativo della deflessione massima effettiva. Per calcolare i carichi più complessi è necessario utilizzare il cosiddetto metodo della doppia integrazione.
Resistenza alla flessione della trave
Per calcolare la deflessione di una trave, è necessario conoscere la resistenza alla flessione della trave e la quantità di forza o carico che influisce sulla flessione della trave. Possiamo definire la resistenza alla flessione della trave moltiplicando il suo modulo di elasticità, E, per il suo momento di inerzia dell'area, I.
Il modulo di elasticità dipende dal materiale della trave. Più alto è il modulo di elasticità di un materiale, più una deflessione può sostenere carichi enormi prima di raggiungere il punto di rottura. Il modulo di elasticità del calcestruzzo è compreso tra 15-50 GPa (gigapascal), mentre l'acciaio tende a essere intorno ai 200 GPa e oltre. Questa differenza nei valori del modulo di elasticità dimostra che il calcestruzzo può sopportare solo una piccola quantità di deflessione e si incrinerà prima dell'acciaio.
Puoi saperne di più sul modulo di elasticità consultando il nostro calcolatore di sforzo e deformazione. D'altra parte, per determinare il momento d'inerzia dell'area per una particolare sezione trasversale della trave, puoi visitare il nostro calcolatore del momento di inerzia. Il momento d'inerzia dell'area rappresenta la resistenza di un materiale al movimento rotatorio, e il valore dipende dalle dimensioni della sezione trasversale del materiale.
Il momento d'inerzia dell'area varia anche a seconda dell'asse lungo il quale il materiale sta ruotando. Per capire meglio questo concetto, consideriamo la sezione trasversale di una trave rettangolare con una larghezza di 20 cm e un'altezza di 30 cm. Utilizzando le formule che puoi vedere anche nel nostro calcolatore per il momento d'inerzia dell'area, possiamo calcolare i valori del momento d'inerzia dell'area trasversale di questa trave come segue:
Iₓ = larghezza × altezza³ / 12,
Iₓ = 20 × (30³)/12,
Iₓ = 45 000 cm⁴; e
Iᵧ = altezza × larghezza³ / 12,
Iᵧ = 30 × (20³)/12,
Iᵧ = 20 000 cm⁴.
Nota che ci sono due valori per il momento d'inerzia dell'area. La ragione è che possiamo considerare che la trave si pieghi verticalmente lungo la campata della trave (o subisca un momento flettente intorno all'asse x) e lateralmente lungo la campata della trave (o si pieghi intorno all'asse y). Poiché stiamo considerando la deflessione della trave quando si piega verticalmente o intorno all'asse x, dobbiamo utilizzare Iₓ per i nostri calcoli.
I valori del momento d'inerzia dell'area ottenuti ci dicono che la trave è più difficile da piegare con un carico verticale e più facile da piegare se sottoposta a un carico laterale orizzontale. Questa differenza nei valori del momento d'inerzia dell'area è il motivo per cui vediamo le travi in questa configurazione — l'altezza è maggiore della larghezza.
Comprendere le formule di deflessione delle travi
Ora che conosciamo i concetti di modulo di elasticità e momento di inerzia dell'area, possiamo capire perché queste variabili sono i denominatori delle formule di deflessione delle travi. Le formule dimostrano che più la trave è rigida, minore sarà la sua deflessione. Tuttavia, esaminando le nostre formule, possiamo anche dire che la lunghezza della trave influisce direttamente sulla sua deflessione. Più la trave è lunga, più può piegarsi e maggiore sarà la sua deflessione.
I carichi, invece, influenzano la deflessione della trave in due modi; la direzione della deflessione e la grandezza della deflessione. I carichi verso il basso tendono a deflettere la trave verso il basso. I carichi possono essere di tipo singolo, di pressione lineare o di momento. Le formule di questo calcolatore si concentrano solo sulle direzioni verso il basso o verso l'alto per il carico puntuale e i carichi distribuiti. I carichi distribuiti sono simili alla pressione, ma considerano solo la lunghezza della trave e non la sua larghezza.
Le formule di questo calcolatore considerano anche il carico di momento o di coppia, sia in senso orario che antiorario. Basta consultare le direzioni delle frecce nell'immagine corrispondente della formula per capire in quali direzioni è presente un valore di carico positivo.
Esempio di calcolo della deflessione di una trave

Per un esempio di calcolo della deflessione di una trave, consideriamo una semplice panca di legno con gambe distanti 1,5 metri l'una dall'altra al centro. Supponiamo di avere una tavola di 4 cm di spessore e 30 cm di larghezza di pino bianco orientale che funge da seduta per questa panchina. Possiamo considerare questo sedile come una trave che si defletterà ogni volta che qualcuno si siederà sulla panchina. Date le dimensioni del sedile, possiamo calcolare il suo momento d'inerzia dell'area, come nell'esempio precedente. Dato che dobbiamo calcolare Iₓ, il suo momento di inerzia dell'area sarà:
Iₓ = larghezza × altezza³ / 12,
Iₓ = 30 × (4³)/12,
Iₓ = 160,0 cm⁴ o 1,6×10-6 m⁴.
Il pino bianco orientale ha un modulo di elasticità di 6800 MPa (6,8×10⁹ Pa), che è il valore che abbiamo ottenuto dal o la guida alle diverse tipologie di legno. Puoi anche ottenere facilmente il valore del modulo di elasticità di altri materiali, come l'acciaio e il cemento, dall'internet o dalla tua biblioteca locale. Ora che conosciamo questi valori, consideriamo il carico che questa panchina dovrà sopportare. Supponiamo che un bambino di 400 N sieda al centro della panchina. Ora possiamo calcolare la deflessione che subirà la seduta della panchina a causa di un carico puntuale al suo centro:
δmax= P × L³ / (48 × E × I),
δmax = (400 N) × (1,5 m)³ / (48 × 6,8×10⁹ Pa × 1,6×10-⁶ m⁴),
δmax= 0,00258 5 m = 2,5850 mm.
Ciò significa che il sedile a panchina si abbasserà di circa 2,6 millimetri rispetto alla sua posizione originale quando il bambino si siede al centro della panchina.
Se hai trovato interessante questo argomento e vuoi saperne di più sulla resistenza dei materiali, ti potrebbe interessare anche il nostro calcolatore per il coefficiente di sicurezza 🇺🇸.
FAQ
Che cos'è la deflessione in ingegneria?
La deflessione in ingegneria si riferisce al movimento di una trave rispetto alla sua posizione originale. Questo movimento può derivare da forze ingegneristiche, sia dalla trave stessa che da una fonte esterna come il peso delle pareti o del tetto. La deflessione in ingegneria è una misura di lunghezza perché quando si calcola la deflessione di una trave, si ottiene un angolo o distanza che si riferisce alla distanza del movimento della trave.
Qual è la formula generale della deflessione della trave?
Le formule generali per la deflessione delle travi sono PL³/(3EI) per le travi a mensola e 5wL⁴/(384EI) per le travi a semplice appoggio, dove P è il carico puntuale, L è la lunghezza della trave, E rappresenta il modulo di elasticità e I si riferisce al momento di inerzia dell'area. Tuttavia, molte altre formule di deflessione consentono agli utenti di misurare diversi tipi di travi e di deflessione.
Come posso calcolare la deflessione di una trave?
Per calcolare la deflessione di una trave segui questi passaggi:
- Determina se si tratta di una trave a mensola o di una trave a semplice appoggio;
- Misura la deflessione della trave dalla deformazione della struttura;
- Scegli la formula di deflessione appropriata per il tuo tipo di trave; e
- Inserisci i tuoi dati tra cui la lunghezza della trave, il momento d'inerzia dell'area, il modulo di elasticità e la forza agente.
Cosa causa la deflessione delle travi?
Le principali cause di deflessione sono il peso posto in cima alla struttura, il momento di inerzia dell'area, che è dato dalle dimensioni della sezione trasversale, dalla lunghezza della struttura non supportata e dal materiale della struttura.
Qual è la deflessione centrale di una trave a semplice appoggio con una luce di 4 m?
3,47 mm, se la lunghezza (L) è 4 m = 4 × 10³ mm, il carico puntuale (P) è 45 × 10³ N, il modulo di elasticità (E) è 2,4 × 10⁵ N/mm² e il momento di inerzia dell'area (I) è 72 × 10⁶ mm⁴. Per calcolare questo valore:
- Scegli la formula: PL³/(48EI); e
- Inserisci i valori:
45 × 10³ × (4 × 10³)³/(48 × 2,4 × 10⁵ × 72 × 10⁶) = 3,47 mm.
