Calculateur de tension
Ce calculateur de tension vous apprendra à déterminer la force de tension qui s'applique aux cordes, fils ou tout élément soumis à une traction. Vous saurez enfin calculer la tension nécessaire pour soulever un objet à l'aide d'une corde et déterminer la tension dans une corde qui tire un objet sur une surface sans frottement. Pour vous aider à comprendre le concept, vous trouverez aussi dans cet article des diagrammes du corps libre (DCL) qui illustrent le calcul de la tension. Si vous voulez en savoir plus sur la tension et la formule de la force de tension, lisez la suite !
Qu'est-ce que la force de tension ?
Imaginez soulever un ballon de basket du sol. Vous sentez son poids dans vos mains à cause de la gravité agissant sur la masse du ballon. Maintenant, attachez une corde autour du ballon et utilisez-la pour le soulever à nouveau. Vous sentez toujours le poids du ballon, mais cette fois, il se transmet par la corde. Dans cette situation, la corde est maintenant en tension. Ce qui maintient la corde ensemble s'appelle la force de tension. En coupant la corde, vous libérez la force de tension et la balle tombe en chute libre.
La force de tension est une force axiale qui passe par un objet qui tire, comme une corde, un fil ou une chaîne. Nous pouvons également observer la force de tension dans d'autres matériaux, comme les tiges et les barres, dès lors qu'ils sont soumis à une traction externe ou à des charges de traction. Les matériaux présentant une résistance à la traction élevée constituent les meilleures tiges et barres, car ils ne se cassent pas facilement lorsqu'ils sont soumis à des forces de tension. Vous pouvez consulter notre calculateur de contrainte 🇺🇸, qui traite de l'élasticité, pour en savoir plus sur la résistance à la traction.
La force de tension est par ailleurs un excellent exemple de la troisième loi de Newton. Cette dernière stipule que lorsqu'un corps exerce une force sur un autre corps, ce dernier exerce une force égale dans la direction opposée sur le corps d'origine. La force de tension est une force réactive qui s'oppose à une force de traction externe.
Deuxième loi de Newton
Pour calculer la tension qui s'exerce sur une corde, il faut d'abord comprendre la deuxième loi de Newton. La deuxième loi de Newton sur le mouvement stipule que la somme des forces agissant sur un objet de masse constante est égale à la masse de cet objet multipliée par son accélération. Nous pouvons également exprimer cette loi sous la forme d'une équation :
ΣF = m × a
où :
- Σ (sigma) – la somme des forces F
- m – la masse de l'objet
- a – l'accélération
Pour un objet suspendu par une corde, nous pouvons utiliser l'accélération gravitationnelle 🇺🇸, g, à la place de a. L'accélération gravitationnelle nous donne la valeur du poids de l'objet en termes de force, comme en newtons ou livres-force. Si l'objet bouge à une accélération différente, nous devrions utiliser son accélération réelle pour le calcul. Cependant, ce calculateur de tension ne détermine les forces de tension que dans les cas d'équilibre statique.
Cela signifie que cet outil ne prend en compte que les objets au repos dans un système donné. Dans ce calculateur de tension, nous supposons également que les cordes n'ont pas de masse et ne contribuent donc pas aux forces de tension. Nous supposons aussi que les masses ou les objets sont dans le vide et ne subissent pas de frottement ou de résistance de l'air par rapport à leur environnement.
Comment déterminer la tension d'une corde tirant un objet ?
La façon de trouver la force de tension sur un objet que l'on tire est la même que lorsque l'objet est suspendu. La seule différence est que nous devons d'abord calculer l'accélération de l'ensemble du système et additionner toutes les forces sur l'axe horizontal. Si la corde est inclinée par rapport au niveau du sol, nous devons également calculer la composante horizontale de la force de traction.
Jetons un coup d'œil à l'exemple ci-dessous pour mieux comprendre comment trouver la force de tension d'une corde tirant un ou deux objets. Dans cet exemple, deux objets sont tirés par une seule force de traction. Une autre corde tire le second objet, qui est attaché au premier, comme indiqué ci-dessous :
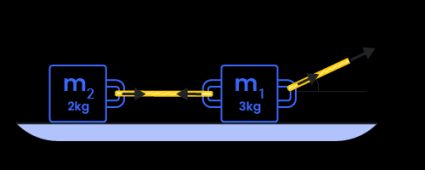
Cette illustration montre que les masses de m₁ et m₂ sont respectivement de 3 kg et 2 kg. La somme de ces deux masses donne la masse totale du système, 5 kg. Nous devons également déterminer la composante horizontale de la force de traction, T = 24 N, qui se trouve à un angle θ = 60°. Si nous utilisons à nouveau les fonctions trigonométriques, nous pouvons dire que la composante horizontale de la force de traction est égale à 24 N × cos(60°), soit 12 N. Maintenant que nous connaissons la composante horizontale de la force de traction et la masse totale du système, nous pouvons calculer l'accélération, a, du système comme suit :
F = m × a → a = F / m
a = 12 N / 5 kg = 2,4 m⋅s-2
Après avoir trouvé l'accélération du système, nous pouvons à nouveau utiliser la deuxième loi de Newton pour calculer la tension de la corde ou du fil du système. Pour ce faire, multipliez l'accélération par la masse que tire la corde. Pour T₂, son diagramme du corps libre nous montre qu'il n'est responsable que de la masse de m₂ ; nous pouvons dire que T₂ = a × m₂, et donc que T₂ = (2,4 m⋅s-2) × (2 kg) = 4,8 N. D'autre part, T₁ est la force de tension qui tire à la fois le poids de m₁ et celui de m₂. Comme nous avons déjà la valeur de T₁, qui est simplement égale à T = 24,0 N, alors nous pouvons en déduire que T₁ = 24,0 N.
Dans notre exemple, si les cordes gauche et droite ne faisaient qu'une, nous pourrions comparer cette configuration à un système de poulie. Une poulie est une machine simple qui prend en compte les forces de tension des cordes pour obtenir un avantage mécanique. Vous pouvez consulter notre calculateur de poulie 🇺🇸 et notre calculateur de longueur de courroie (qui est un système à deux poulies) pour en savoir plus sur l'avantage mécanique et la tension.
FAQ
Comment calculer la tension d'une corde à un angle ?
Pour calculer la tension d'une corde à un angle :
- Trouvez l'angle par rapport à l'axe horizontal auquel la corde est placée.
- Trouvez la composante horizontale de la force de tension en multipliant la force appliquée par le cosinus de l'angle.
- Déterminez la composante verticale de la force de tension en multipliant la force appliquée par le sinus de l'angle.
- Additionnez ces deux forces pour obtenir l'intensité totale de la force appliquée.
- Tenez compte de toute autre force appliquée, par exemple une autre corde, la gravité ou le frottement, et résolvez l'équation de la force normalement.
Comment calculer la tension produite par une boîte de 10 kg sur deux cordes suspendues à 60° ?
Pour déterminer la tension dans ce cas :
- Déterminez les composantes verticales et horizontales des forces de traction sur les cordes :
- T₁ = T₁ sin(60) + T₁ cos(60)
- T₂ = T₂ sin(60) + T₂ cos(60)
- Les composantes verticales (sinus) équilibrent le poids :
- T₁ sin(60) + T₂ sin(60) = √3 (T₁ + T₂)/2 = 98 N
- Les composantes horizontales (cosinus) de la force de tension s'équilibrent :
- T₁ cos(60) = T₂ cos(60) ou T₁ = T₂
- Résolvez les équations :
- 98 N = √3 T₁ ou, T₁ = T₂ = 56,58 N
Comment calculer la tension de deux cordes ayant le même angle de suspension ?
Lorsque les angles de suspension (α) sont les mêmes pour deux cordes, l'intensité de la tension (T) est la même pour les deux cordes. Pour déterminer l'intensité de la tension, utilisez l'équation 2T sin(α) = m × g, où m × g représente le poids de l'objet suspendu.
La tension est-elle une force de contact ?
Oui, la tension est une force de contact. La tension se produit dans une corde ou un câble lorsqu'ils sont étirés, et les forces de traction sont transmises à travers la corde d'une extrémité à l'autre.

Comment calculer la tension des cordes qui suspendent un objet ?
Nous pouvons voir dans l'illustration ci-dessous que la force, F, nécessaire pour soulever l'objet est égale au poids, W, de l'objet. Cette idée est au cœur de notre formule de force de tension. Vous trouverez également ci-dessous le diagramme du corps libre de l'objet, qui montre les forces de tension, T, agissant sur la corde. Comme vous pouvez le constater, les forces de tension agissent par paires et dans des directions opposées :
Conformément à la deuxième loi de Newton, nous pouvons alors exprimer la somme des forces à l'aide de diagrammes du corps libre de l'objet, comme le montre la partie droite de l'illustration ci-dessus. On parle aussi d'isolement d'un solide lorsque l'on représente un objet seul avec les forces extérieures s'exerçant sur lui. Nous utilisons les diagrammes du corps libre pour montrer les différentes directions et intensités des forces qui agissent sur un corps. En situation d'équilibre, ces forces doivent toutes être égales à zéro. Si l'on considère que toutes les forces ascendantes sont positives et que toutes les forces descendantes sont négatives, notre équation est la suivante :
ΣF↑ = 0 = T + (-W)
T = W
Ici, le poids, W, devient négatif puisqu'il est dirigé vers le bas. En transposant W de l'autre côté de l'équation, nous pouvons maintenant voir que la force de tension dans la corde est égale au poids de l'objet qu'elle porte, comme cela a également été montré ci-dessus.
Si nous utilisons plusieurs cordes pour soulever l'objet, la force de tension totale est divisée entre les cordes. La force de tension dans chaque corde dépend de son angle par rapport à la direction de la force à laquelle elle s'oppose. Pour mieux comprendre cela, considérons un autre diagramme du corps libre d'un objet suspendu par deux cordes, comme illustré ci-dessous :
Dans le diagramme du corps libre ci-dessus, nous pouvons voir les composantes horizontale et verticale des forces de tension, T₁ et T₂. Les forces sont des vecteurs, ce qui signifie qu'elles ont toujours une norme et une direction. Comme tous les vecteurs, les forces peuvent être exprimées par ces composantes, qui donnent la mesure de la force le long des axes horizontal et vertical. T₁ₓ et T₂ₓ sont les composantes horizontales de T₁ et T₂, respectivement. De leur côté, T1y et T2y sont les composantes verticales des mêmes forces, respectivement. Comme la gravité agit sur l'objet le long de l'axe vertical, nous devons prendre en compte les composantes verticales des forces de tension pour notre sommation des forces comme suit :
ΣF↑ = 0 = T1y + T2y + (-W)
W = T1y + T2y
Comme nous connaissons également les angles des forces de tension, nous pouvons exprimer T1y et T2y en termes de T₁ et T₂, respectivement, à l'aide de fonctions trigonométriques :
T1y = T₁ × sin(α)
T2y = T₂ × sin(β)
W = T₁ × sin(α) + T₂ × sin(β)
Nous pouvons également dire que pour que le système soit en équilibre, l'objet ne doit pas se déplacer horizontalement ou le long de l'axe x. Par conséquent, les composantes horizontales de T₁ et T₂ doivent être égales à zéro. En outre, à l'aide de la trigonométrie, nous pouvons exprimer T₁ₓ et T₂ₓ en termes de T₁ et T₂, respectivement :
T₁ₓ = T₂ₓ
T₁ × cos(α) = T₂ × cos(β)
Si nous divisons les deux côtés par cos(α), nous obtenons une équation dans laquelle T₁ est exprimé en termes de T₂ et des angles :
T₁ = T₂ × cos(β) / cos(α)
Nous pouvons ensuite utiliser cette équation pour résoudre T₂ en remplaçant T₂ × cos(β) / cos(α) par T₁ dans notre équation de somme des forces, comme indiqué ci-dessous :
W = T₁ × sin(α) + T₂ × sin(β)
W = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)
W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]
T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]
Enfin, si nous multiplions toute cette équation par cos(β) / cos(α) après avoir déduit la valeur de T₁ en termes de T₂, puis en simplifiant le tout, nous obtenons cette équation :
T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]
t₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]
T₁ = W / [cos(α) × sin(β) / cos(β) + sin(α)]
Il ne vous reste plus qu'à connaître les angles des cordes par rapport à l'axe horizontal. Si un angle par rapport à l'axe vertical est donné, il suffit de soustraire cet angle de 90°. Vous obtiendrez ainsi l'angle par rapport à l'axe horizontal. Toutefois, si l'on vous donne d'autres valeurs d'angles qui peuvent être supérieures à 90° ou même à 180°, vous pouvez consulter notre calculateur d'angle de référence pour vous aider à déterminer l'angle dont vous avez besoin. Après avoir déterminé les valeurs des variables dans nos formules de force de tension, nous pouvons maintenant résoudre les forces de tension.