Calculateur d'angle de référence

Notre calculateur d'angle de référence est un outil pratique pour calculer l'angle aigu formé par le côté terminal d'un angle trigonométrique et l'axe des abscisses. Il suffit d'entrer un angle positif dans le premier champ et le calculateur trouvera l'angle de référence pour vous. Grâce à cet article, vous pourrez également découvrir la définition d'un angle de référence.

De plus, nous vous expliquerons les démarches nécessaires pour trouver un angle de référence en radians et en degrés, en fournissant quelques exemples. Et pour finir, nous vous montrerons des graphiques à quadrants !

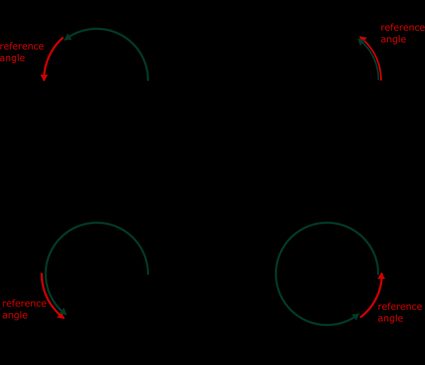
Regardez l'image ci-dessus. Dans chaque cas, l'angle mesuré se trouve entre l'axe des abscisses et le côté terminal (le côté délimitant l'angle) de l'angle donné. Si vous voulez trouver l'angle de référence d'un angle donné, vous devez trouver le plus petit angle possible formé par l'axe des abscisses et le côté terminal. L'angle de référence est toujours mesuré dans le sens antihoraire.

Les angles de référence sont utiles en trigonométrie. Si vous voulez trouver le sinus ou le cosinus d'un angle quelconque, vous devez d'abord trouver son angle de référence. Ensuite, vous pouvez calculer la fonction trigonométrique de l'angle de référence et choisir le bon signe.

Les angles les plus courants et leurs fonctions trigonométriques sont indiqués dans le tableau ci-dessous :

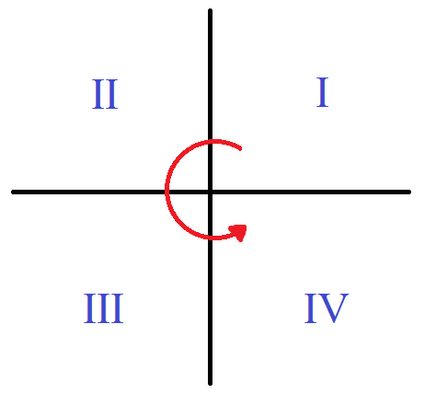
Les deux axes d'un système de coordonnées cartésiennes bidimensionnel (2D) divisent le plan en quatre parties infinies appelées quadrants. La numérotation des quadrants commence dans le quadrant en haut à droite, où les deux coordonnées, x et y, sont positives, et se poursuit dans le sens antihoraire, comme sur l'image.

En général, les valeurs des fonctions trigonométriques (sinus, cosinus, tangente, cotangente) d'un angle donné et de son angle de référence sont égales. Le signe est le seul à changer : ces fonctions deviennent positives ou négatives selon le quadrant. Voici une règle mnémotechnique qui vous aidera à vous rappeler quand ces fonctions sont positives :

« Tous Savent Tout Calculer » (TSTC)

• T pour toutes. Dans le premier quadrant, toutes les fonctions trigonométriques ont des valeurs positives.
• S pour sinus. Dans le deuxième quadrant, seule la fonction sinus est positive.
• T pour tangente. Dans le troisième quadrant, la tangente et la cotangente ont des valeurs positives.
• C pour cosinus. Dans le quatrième quadrant, seule la fonction cosinus est positive.

N'oubliez pas de jeter un coup d'œil à notre calculateur de la loi des cosinus 🇺🇸 et au calculateur de la loi des sinus 🇺🇸 pour obtenir plus d'informations sur la trigonométrie.

Il vous suffit de suivre les étapes ci-dessus :

1. Choisissez votre angle initial, par exemple, 610°.

2. Si votre angle est supérieur à 360° (un angle complet), continuez à soustraire 360° jusqu'à ce que vous obteniez un angle inférieur à un angle complet. Cela équivaut à l'opération modulo. Dans cet exemple, après avoir soustrait 360°, nous obtiendrons 250°.

3. Déterminez dans quel quadrant se trouve votre angle :

   • de 0° à 90° – premier quadrant
   • de 90° à 180° – deuxième quadrant
   • de 180° à 270° – troisième quadrant
   • de 270° à 360° – quatrième quadrant

   Dans notre cas, 250° se situe dans le troisième quadrant.

4. Choisissez la formule correcte pour calculer l'angle de référence :

   • de 0° à 90° – angle de référence = angle
   • de 90° à 180° – angle de référence = 180° - angle
   • de 180° à 270° – angle de référence = angle - 180°
   • de 270° à 360° – angle de référence = 360° - angle

   Dans ce cas, nous devons choisir la formule angle de référence = angle - 180°.

5. Insérez votre angle dans l'équation pour trouver l'angle de référence de votre angle :

   angle de référence = 250° - 180° = 70°

Si vous avez besoin d'un outil pour vous aider à convertir les différentes unités de mesure des angles, essayez notre calculateur de conversion d'angles 🇺🇸.

C'est plus facile qu'il n'y paraît !

1. Pour les angles supérieurs à 2π, continuez à soustraire 2π jusqu'à ce que vous obteniez une valeur inférieure à un angle complet.
2. Déterminez le quadrant :

• de 0 à π/2 – premier quadrant, donc angle de référence = angle
• de π/2 à π – deuxième quadrant, donc angle de référence = π - angle
• de π à 3π/2 – troisième quadrant, donc angle de référence = angle - π
• de 3π/2 à 2π – quatrième quadrant, donc angle de référence = 2π - angle

Comme vous pouvez le voir, qu'il s'agisse de degrés ou de radians, les étapes à suivre sont similaires. Considérons à titre d'exemple un angle mesurant 28π/9 radians.

1. Après avoir soustrait des multiples de 2π, il nous reste 10π/9.

2. 10π/9 est un peu plus grand que π ; il se trouve donc dans le troisième quadrant. La formule d'angle de référence à utiliser dans ce cas est :

   angle de référence = angle - π = π/9

C'est simple comme bonjour ! Voici ce qu'il faut faire pour calculer un angle de référence à l'aide de ce calculateur :

1. Saisissez votre angle dans le premier champ. Vous pouvez choisir n'importe quel angle positif. Disons que nous voulons trouver l'angle de référence de l'angle de 210°. Si vous le souhaitez, vous pouvez également convertir les unités, par exemple en radians.
2. C'est tout ! Le calculateur d'angle de référence a trouvé l'angle aigu entre l'axe des abscisses et le côté terminal de votre angle, ainsi que le quadrant dans lequel se trouve cet angle. Notre angle de référence mesure 30° et il se trouve dans le troisième quadrant. Génial, n'est-ce pas ?

Si vous cherchez une réponse rapide, consultez la liste ci-dessous :

Premier quadrant :

Deuxième quadrant :

Troisième quadrant :

Quatrième quadrant :