Calculateur d'hexagone

Bienvenue sur le calculateur d'hexagone, un outil pratique pour analyser tout hexagone régulier. L'hexagone est l'une des formes les plus répandues dans la nature, du nid d'abeille en passant par les carreaux pour miroir – ses usages sont presque infinis. Nous expliquons ici non seulement pourquoi ce polygone à 6 côtés est si populaire, mais aussi comment dessiner correctement les côtés d'un hexagone. Nous répondons également à la question « qu'est-ce qu'un hexagone ? » en utilisant la définition de l'hexagone.

Avec notre calculateur d'hexagone, vous pouvez explorer de nombreuses propriétés et opérations géométriques, notamment comment trouver l'aire d'un hexagone, mais aussi apprendre à utiliser le calculateur pour simplifier toute analyse impliquant cette forme à 6 côtés.

Il n'est pas surprenant que l'hexagone (également connu sous le nom de « polygone à 6 côtés ») ait précisément six côtés. C'est vrai pour tous les hexagones puisqu'il s'agit de leur caractéristique principale. La longueur des côtés peut varier au sein d'un même hexagone, sauf dans le cas de l'hexagone régulier, dont tous les côtés doivent avoir la même longueur.

Nous nous pencherons un peu plus sur ce type de forme plus tard, lorsque nous verrons comment trouver l'aire d'un hexagone. Pour l'instant, il suffit de dire que l'hexagone régulier est le plus courant des polygones à 6 côtés et celui que l'on trouve le plus souvent dans la nature.

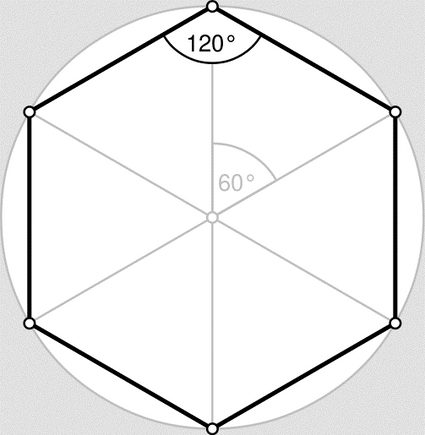
Une section entière sera consacrée aux propriétés importantes de la forme hexagonale régulière, mais nous devons d'abord répondre à la question : « Qu'est-ce qu'un hexagone ? » Cela nous aidera à comprendre les astuces que nous pouvons utiliser pour calculer l'aire d'un hexagone sans utiliser la formule de l'aire de l'hexagone à l'aveuglette. Ces astuces consistent à utiliser d'autres polygones tels que les carrés, les triangles et même les parallélogrammes.

Comme nous l'avons déjà mentionné, l'hexagone régulier doit avoir tous ses côtés de même longueur et tous ses angles internes doivent être égaux. Chaque longueur de côté peut servir individuellement (tant que les 6 côtés ont bien la même longueur !), pour calculer le périmètre d'un hexagone. C'est si simple que vous n'avez même pas besoin du calculateur du périmètre d'un polygone 🇺🇸. Il vous suffit de calculer :

• périmètre = 6 × côté

Les angles d'un hexagone arbitraire peuvent avoir n'importe quelle valeur, mais leur somme doit être de 720º (vous pouvez facilement les convertir en d'autres unités à l'aide de notre calculateur de conversion d'angles 🇺🇸). Comme l'hexagone régulier exige que tous ses angles soient égaux, il s'ensuit que chaque angle doit être de 120º. Ce fait s'avère de la plus haute importance lorsque nous parlerons de la prédominance de la forme hexagonale dans la nature. Il sera également utile lorsque nous expliquerons comment trouver l'aire d'un hexagone régulier et sa formule géométrique.

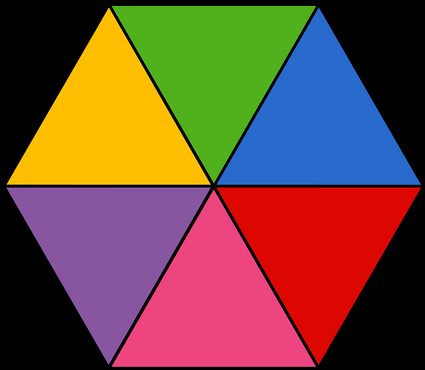
Nous allons maintenant voir comment trouver l'aire d'un hexagone en utilisant différentes astuces. Le plus simple est d'utiliser notre calculateur d'hexagone, qui comprend un outil de conversion d'aire intégré. Pour ceux qui veulent le faire à la main, nous allons expliquer comment trouver l'aire d'un hexagone régulier avec et sans sa formule. La formule pour calculer l'aire d'un polygone est toujours la même, quel que soit le nombre de côtés, tant qu'il s'agit d'un polygone régulier :

• aire = apothème × périmètre / 2

Pour rappel, l'apothème est la distance entre le milieu d'un côté et le centre. Vous pouvez le considérer comme la hauteur du triangle équilatéral – triangle formé en prenant un côté et deux rayons de l'hexagone (chacune des zones colorées dans l'image ci-dessus). On peut aussi considérer l'apothème comme la distance entre le centre et n'importe quel côté de l'hexagone puisque la distance euclidienne est définie à l'aide d'une droite perpendiculaire.

Si vous ne vous souvenez pas de la formule, vous pouvez toujours penser au polygone à 6 côtés comme à une collection de 6 triangles. Pour l'hexagone régulier, ces triangles sont des triangles équilatéraux. Il est donc beaucoup plus facile de calculer leur aire que s'il s'agissait de triangles isocèles ou même de triangles rectangles isocèles comme c'est le cas pour un carré.

Pour le triangle équilatéral, tous les côtés ont la même longueur, qui correspond à la longueur du côté de l'hexagone qu'ils forment. Nous l'appellerons a. Et la hauteur d'un triangle sera h = √3/2 × a, qui est la valeur exacte de l'apothème dans ce cas. Nous vous rappelons que √ signifie racine carrée. Grâce à cela, nous pouvons commencer les calculs :

• A₀ = a × h / 2
• = a × √3/2 × a / 2
• = √3/4 × a²

Où A₀ désigne l'aire de chacun des triangles équilatéraux qui composent l'hexagone. Après avoir multiplié cette aire par six (car nous avons 6 triangles), nous obtenons la formule de l'aire de l'hexagone :

• A = 6 × A₀ = 6 × √3/4 × a²
• A = 3 × √3/2 × a²
• = (√3/2 × a) × (6 × a) /2
• = apothème × périmètre /2

Nous espérons que vous pouvez voir comment nous arrivons à la même formule que l'aire d'un hexagone que nous avons mentionnée précédemment.

Si vous souhaitez faire preuve d'exotisme, vous pouvez jouer avec d'autres formes. Par exemple, supposons que vous divisez l'hexagone en deux (d'un sommet à l'autre). Dans ce cas, vous obtenez deux trapèzes, et vous pouvez calculer l'aire de l'hexagone comme étant la somme de ces deux trapèzes. Vous pouvez aussi combiner deux triangles adjacents pour construire un total de trois losanges et calculer l'aire de chacun d'eux séparément. Vous pouvez même décomposer l'hexagone en un grand rectangle (en utilisant les diagonales courtes) et deux triangles isocèles !

N'hésitez pas à jouer avec différentes formes et calculateurs pour trouver d'autres astuces. Essayez d'utiliser uniquement des triangles rectangles ou même des triangles rectangles spéciaux pour calculer l'aire d'un hexagone !

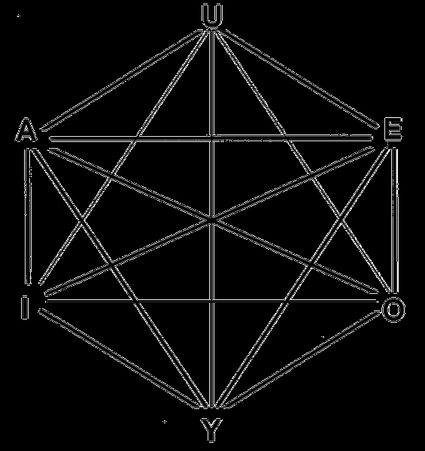
Le nombre total de diagonales d'un hexagone est de 9 – trois d'entre elles sont de longues diagonales qui traversent le point central, et les six autres constituent ce que l'on appelle la « hauteur » de l'hexagone.
Notre calculateur d'hexagone peut aussi vous épargner certains calculs fastidieux sur les longueurs des diagonales. Voici comment calculer les deux types de diagonales :

• Diagonales longues – elles traversent toujours le point central de l'hexagone. Comme vous pouvez le remarquer sur l'image ci-dessus, la longueur d'une telle diagonale est égale à deux longueurs d'arêtes :

  D = 2 × a

• Diagonales courtes – elles ne traversent pas le point central. Elles sont construites en joignant deux sommets, en laissant exactement un sommet entre eux. Leur longueur est égale à d = √3 × a.

Une autre paire de mesures importantes dans un hexagone sont le rayon circonscrit et le rayon inscrit. Le rayon circonscrit est le rayon du cercle qui contient tous les sommets de l'hexagone régulier. Le rayon inscrit est le rayon du plus grand cercle contenu entièrement dans l'hexagone.

• Rayon circonscrit – pour trouver le rayon d'un cercle circonscrit d'un hexagone régulier, vous devez déterminer la distance entre le point central de l'hexagone (qui est aussi le centre du cercle) et l'un des sommets. Il est simplement égal à R = a.

• Rayon inscrit – le rayon d'un cercle inscrit dans l'hexagone régulier est égal à la moitié de sa hauteur, qui est aussi l'apothème : r = √3/2 × a.

Nous allons maintenant explorer un monde plus pratique et moins mathématique : comment dessiner un hexagone. Pour un hexagone aléatoire (irrégulier), la réponse est simple : dessine n'importe quelle forme à 6 côtés de façon à ce que ce soit un polygone fermé, et c'est tout. Mais pour un hexagone régulier, les choses ne sont pas si simples puisqu'il faut s'assurer que tous les côtés ont la même longueur.

Pour obtenir un résultat parfait, vous aurez besoin d'un compas. Dessinez un cercle et, avec le même rayon, commencez à faire des repères le long de celui-ci. En partant d'un point aléatoire, puis en faisant le repère suivant en utilisant le précédent repère comme point d'ancrage, dessinez un cercle avec le compas. Vous obtiendrez 6 repères, et si vous les reliez avec des lignes droites, vous obtiendrez un hexagone régulier. Vous pouvez voir un processus similaire dans l'animation ci-dessus.

Notre calculateur Omni d'hexagone vous permet de calculer plusieurs paramètres intéressants du polygone à 6 côtés. L'utilisation de ce calculateur est simple comme bonjour. Un seul des paramètres est nécessaire pour calculer tous les autres et il comprend un outil de conversion de longueur intégré pour chacun d'entre eux.

Nous avons déjà abordé tous les paramètres du calculateur, mais dans un souci de clarté et d'exhaustivité, nous allons maintenant les passer brièvement en revue :

• Aire – surface 2D délimitée par la forme de l'hexagone 
• Longueur des côtés – distance entre un sommet et le sommet suivant 
• Périmètre – somme des longueurs de tous les côtés de l'hexagone
• Diagonale longue — distance d'un sommet à celui opposé
• Diagonale courte – distance entre deux sommets ayant un seul sommet entre eux
• Rayon du cercle circonscrit – distance entre le centre et un sommet (identique au rayon de l'hexagone)
• Rayon du cercle inscrit – identique à l'apothème

Tout le monde aime les exemples d'applications concrètes, avec les hexagones, vous n'allez pas être déçu·e ! Ils sont certainement l'un des polygones les plus utilisés au monde. En commençant par les utilisations humaines, la plus simple (et probablement la moins excitante) est l'utilisation de carreaux hexagonaux pour le revêtement de sol. Les hexagones sont une excellente forme parce qu’ils s’adaptent parfaitement les uns aux autres pour couvrir n'importe quelle surface. Si vous êtes intéressé par une telle utilisation, nous vous recommandons le calculateur de revêtement de sol et le calculateur de superficie 🇺🇸, qui sont d'excellents outils pour cela.

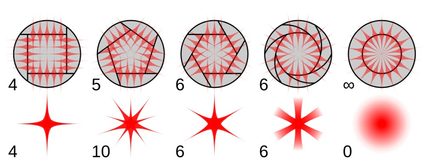
Le cas suivant est commun à tous les polygones, mais il est tout de même intéressant à voir. En photographie, l'ouverture du capteur a presque toujours une forme polygonale. Cette partie de l'appareil photo influe sur les nombreuses propriétés et caractéristiques des images produites par un appareil photo. La caractéristique plus inattendue est la forme des objets très lumineux (en forme de point) due à l'effet appelé réseau de diffraction, et elle est illustrée dans l'image ci-dessus.

L'une des utilisations les plus précieuses des hexagones à l'ère moderne, étroitement liée à celle dont nous avons parlé pour la photographie, est l'astronomie. L'un des plus gros problèmes que nous rencontrons lorsque nous observons des étoiles lointaines est leur faible luminosité dans le ciel nocturne. En effet, bien qu'il s'agisse d'objets très brillants, ils sont tellement éloignés que seule une infime partie de leur lumière nous parvient ; vous pouvez en savoir plus à ce sujet avec notre calculateur de luminosité 🇺🇸. En plus de cela, en raison d'effets relativistes (similaires à la dilatation du temps et à la contraction des longueurs), leur lumière arrive sur la Terre avec moins d'énergie qu'elle n'a été émise. Cet effet s'appelle le décalage rouge.

Le résultat est que nous obtenons une toute petite quantité d'énergie avec une longueur d'onde plus importante que ce que nous souhaiterions. La meilleure façon de contrer ce phénomène est de construire des télescopes aussi énormes que possible. Le problème est qu'il est pratiquement impossible de fabriquer une lentille ou un miroir d'une seule pièce de plus de deux mètres, sans parler des problèmes de logistique. La solution consiste à construire un miroir modulaire à l'aide de carreaux hexagonaux comme celles que vous pouvez voir sur les photos ci-dessus.

La fabrication d'un miroir aussi grand améliore la résolution angulaire du télescope, ainsi que le facteur de grossissement grâce aux propriétés géométriques d'un « télescope de Cassegrain ». Nous pouvons donc dire que grâce aux hexagones réguliers, nous pouvons mieux voir, plus loin et plus clairement que nous n'aurions jamais pu le faire avec des lentilles ou des miroirs d'une seule pièce.

Savez-vous que les dessus-de-lit hexagonaux existent aussi ? Découvrez-en plus avec le calculateur de couettes hexagonales 🇺🇸 d'Omni !

Le motif en nid d'abeille est composé d'hexagones réguliers disposés côte à côte. Ils remplissent entièrement la surface qu'ils recouvrent, il n'y a donc pas d'espace entre eux. Ce motif en nid d'abeilles apparaît non seulement dans les ruches d'abeilles (quelle surprise !) mais aussi dans de nombreux autres endroits dans la nature. En fait, il est si populaire que l'on pourrait dire que c'est la forme par défaut lorsque des forces contradictoires sont en jeu et que la forme sphérique n'est pas possible en raison de la nature du problème.

Des 'ruches' d'abeilles aux fissures des rochers en passant par la chimie organique (même dans les éléments constitutifs de la vie : les protéines), les hexagones réguliers sont la forme polygonale la plus répandue dans la nature. Et il y a une raison à cela : les angles de l'hexagone. L'angle de 120º est le plus stable mécaniquement de tous et, par coïncidence, c'est aussi l'angle auquel les côtés se rejoignent au niveau des sommets lorsque l'on aligne des hexagones côte à côte. Pour une description complète de l'importance et des avantages des hexagones réguliers, nous vous recommandons de regarder cette vidéo.

La manière dont les angles de 120º répartissent les forces (et, par conséquent, les tensions) entre 2 des côtés de l'hexagone en fait une géométrie très stable et mécaniquement efficace. C'est un avantage important des hexagones. Une autre propriété importante des hexagones réguliers est qu'ils peuvent remplir une surface sans espace entre eux (tout comme les triangles et les carrés réguliers). De plus, la forme régulière à 6 côtés a le plus petit périmètre pour la plus grande surface parmi tous les polygones, ce qui la rend très efficace.

Un exemple fascinant dans cette vidéo est celui des bulles de savon. Lorsque vous créez une bulle avec de l'eau, du savon et un peu de votre souffle, elle a toujours une forme sphérique. Cela est dû au fait que le volume d'une sphère est le plus grand de tous les objets pour une surface donnée.

Cependant, lorsque nous disposons les bulles ensemble sur une surface plane, la sphère perd son avantage en termes d'efficacité puisque la section d'une sphère ne peut pas recouvrir complètement un espace en 2D. La forme suivante la plus performante en termes de rapport volume/surface se trouve également être la meilleure pour équilibrer la tension inter-bulles qui se crée à la surface des bulles. Il s'agit bien sûr de notre magnifique hexagone.

Les bulles présentent une façon intéressante de visualiser les avantages de l'hexagone par rapport à d'autres formes, mais ce n'est pas la seule. Dans la nature, comme nous l'avons mentionné, il y a beaucoup d'exemples de formations hexagonales, le plus souvent dues à des contraintes et des tensions dans le matériau. Malheureusement, nous ne pouvons pas tous les passer en revue. Nous pouvons cependant nommer quelques endroits où l'on peut trouver des motifs hexagonaux réguliers dans la nature :

• les ruches d'abeilles ;
• les composés organiques ;
• les amas de bulles ;
• les formations rocheuses (comme celle de la Chaussée des Géants) ;
• les yeux des insectes ;
• etc.