Calculateur de croissance exponentielle

Il existe un nombre important de processus pour lesquels vous pouvez utiliser ce calculateur de croissance exponentielle. Tout d'abord, jetons un coup d'œil à la formule de croissance exponentielle :

En règle générale, elle est utilisée lorsqu'une quantité ayant une valeur initiale, $x_0$, évolue dans le temps, $t$, avec un taux de variation constant, $r$. La fonction exponentielle apparaissant dans la formule ci-dessus a une base égale à $1 + r/100$.

Notez que le taux de croissance exponentielle, $r$, peut être n'importe quel nombre positif, mais ce calculateur fonctionne également comme un calculateur de décroissance exponentielle, où $r$ représente également le taux de décroissance, qui doit être compris entre 0 et -100 %. La raison en est que vous ne pouvez pas avoir une décroissance de plus de 100 % par rapport à la quantité initiale, car cela donnerait une valeur négative.

L'équation de croissance exponentielle est utilisée en datation au radiocarbone 🇺🇸, en PCR (vous pouvez découvrir pourquoi avec notre calculateur de température d'hybridation 🇺🇸), ainsi que pour calculer des intérêts composés. Pour en savoir plus, consultez notre calculateur d'intérêts composés. Vous trouverez ci-dessous d'autres exemples d'utilisation de cette formule.

Considérez le problème suivant : la population d'une petite ville au début de l'année 2019 était de 10 000 personnes. On a remarqué que la population de la ville augmente à un rythme régulier de 5 % par an. Que devez-vous faire pour calculer la taille prévisionnelle de la population en 2030 ? D'après les données fournies, nous savons que la valeur initiale de la population, $x_0$, est de 10 000. Et nous avons un taux de croissance de $r = 5$.

Par conséquent, la formule de croissance exponentielle que nous devons utiliser est la suivante :

Ici, $t$ représente le nombre d'années écoulées depuis 2019. Dans notre cas, pour l'année 2030, il faut utiliser $t = 11$, puisque c'est la différence du nombre d'années entre 2030 et l'année initiale 2019. Finalement, nous obtenons :

Ainsi, le nombre prévisionnel d'habitants de notre petite ville en 2030 est d'environ 17 103.

Si vous souhaitez approfondir un peu plus cette formule particulière, vous pouvez utiliser notre calculateur de croissance exponentielle pour connaître le nombre prévisionnel d'habitants pour chaque année, à partir de 2019. Ce calcul donne le tableau suivant, où nous arrondissons les résultats à l'entier le plus proche :

Si vous souhaitez avoir une meilleure idée de la croissance de la population, vous pouvez représenter ces données sous forme de graphique. L'axe horizontal représente l'axe du temps et l'axe vertical, la valeur de la population $x(t)$. Les données du tableau sont tous des points situés sur le graphe continu de la fonction de croissance exponentielle :

Étant donné que la base de cette fonction exponentielle est 1,05, et qu'elle est supérieure à 1, le graphique de croissance exponentielle que nous obtenons est croissant. La principale différence entre ce graphique et celui de la fonction exponentielle normale est que son ordonnée à l'origine n'est pas de 1, mais de 10 000, ce qui correspond à la valeur initiale $x_0$:

Cet exemple montre les limites possibles du modèle de croissance exponentielle — il est irréaliste que le taux de croissance reste constant au fil du temps. En d'autres termes, il est difficile de s'attendre à ce que le taux de croissance annuel de la population de la ville reste à 5 % pendant une décennie ou plus.

En situation réelle, il existe des oscillations naturelles du taux de croissance qui ne sont pas prises en compte dans ce modèle de croissance exponentielle. Un modèle de croissance de la population plus réaliste est le modèle de croissance logistique, qui comporte la capacité de charge, une constante représentant la limite de croissance naturelle de la population.

En continuant avec notre petite ville, la question suivante que vous pouvez vous poser est la suivante : « quand pouvons-nous nous attendre à ce que la population atteigne une valeur importante ? » Cela est utile si vous voulez savoir quand adapter l'urbanisme de la ville à une population plus importante. Le conseil municipal doit donc savoir en quelle année il peut s'attendre à ce que la population de la ville triple par rapport aux 10 000 habitants d'origine.

Ici, nous savons combien vaut $x(t)$, mais nous ne connaissons pas la valeur de $t$ quand cela se produira. Procédons étape par étape.

1. Inscrivez $x(t) = 30\, 000$ dans la formule : $30\,000 = 10\, 000 \times 1,\!05^{t}$

2. Après avoir divisé les deux côtés de l'équation par 10 000, on obtient : $1,\!05^{t} = 3$

3. Prenez le logarithme en base 1,05 des deux côtés de cette équation : $t = \log_{1,05} 3$

4. Utilisez le logarithme pour finalement obtenir : $t = 22,\!52$

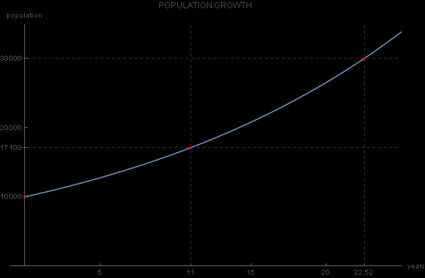
Donc, la réponse à la question du conseil est d'environ 22 ans. La population aura triplé en 2041, par rapport à l'année initiale de 2019.

Vous avez peut-être déjà remarqué un problème lié à la croissance exponentielle et la décroissance, à savoir qu'elles traitent naturellement le temps comme une valeur uniquement positive, nous permettant ainsi de prédire une quantité future. Cependant, cela ne nous empêche pas d'utiliser cette formule avec des valeurs temporelles négatives. Cela signifie que nous décrivons le phénomène qui nous intéresse dans le temps avant que l'observation initiale n'ait été faite.

Dans le cas de la croissance de la population, vous pourriez vous poser la question suivante : quelle était la population de notre petite ville en 2000, en supposant que le taux de croissance de la population était constant à 5 % ?

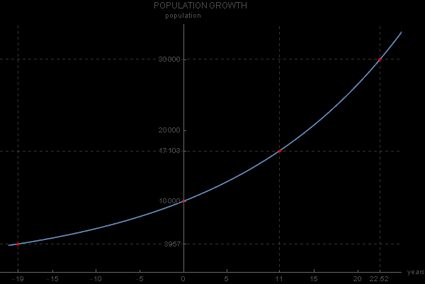
Pour résoudre cette question, vous utiliseriez $t = -19$, puisque l'année 2000 précède l'année 2019 de 19 ans :

La réponse serait donc 3 957 habitants, comme vous pouvez le voir sur ce graphique :

Pour certaines applications, par exemple lors du calcul de la décroissance exponentielle d'une substance radioactive, une autre façon d'écrire la formule de croissance et de décroissance exponentielle est plus productive :

Le coefficient $k$ joue le rôle du taux de croissance, de manière similaire à $r$ dans la formule originale de croissance exponentielle. En comparant l'équation ci-dessus avec l'équation originale, vous pouvez voir que la relation entre $r$ et $k$ est la suivante :

Cela qui signifie que :

$r = 100 \times (e^k- 1)$ et $k = \ln(1 + r/100)$

La décroissance radioactive est un exemple bien connu d'utilisation de la formule de décroissance exponentielle. Pour une quantité initiale donnée de substance radioactive, vous pouvez établir la loi qui régit sa décroissance dans le temps. Cependant, un exemple peut-être plus amusant consiste à mesurer la quantité de café qui reste dans votre corps à 22 heures si vous avez bu une tasse de café avec $x_0 = 95\ \rm mg$ de caféine à midi.

Nous utiliserons le fait que la demi-vie de la caféine dans le corps humain est d'environ six heures. La demi-vie est définie comme le temps nécessaire pour qu'une quantité donnée diminue de moitié par rapport à sa valeur initiale. Ainsi, dans cet exemple, nous avons :

$x(6) = 1/2 \times 95 \text{ mg} = 47,\!5 \text{ mg}$

Ici, il sera plus facile d'utiliser la notation alternative pour la formule de la croissance exponentielle :

$x(t) = 95 \times e^{kt}$

Voici le calcul étape par étape :

1. Entrez x(6)= 47,5 et t = 6 dans l'équation : $47,\!5 = 95 \times e^{6k}$

2. Cette expression, après avoir divisé les deux côtés de l'équation par 95 et appliqué le logarithme naturel, donne : $6\times k = \ln 0,\!5$

3. En utilisant le logarithme naturel, on obtient : $k = -0,\!115 5$

4. Par conséquent, la formule de décroissance exponentielle dans notre exemple est : $x(t) = 95 \times e^{-0,115\,5 \times t}$

5. Puisque 22 heures est dix heures plus tard que midi, nous voulons connaître la quantité de caféine à t = 10. Nous avons : $x(10) = 95 \times e^{-0,115\,5 \times 10} = 29,\!930\,5$

Ainsi, à 22 heures, la quantité de caféine restant dans votre corps sera d'environ 30 mg.

Le temps peut être exprimé dans pratiquement n'importe quelle unité appropriée. Pour certains problèmes, il s'agira de secondes, pour d'autres, d'années. Vous devriez choisir l'unité de temps de manière à correspondre à la nature du processus observé. Par exemple, si vous souhaitez comprendre l'évolution de la population d'une ville, vous devriez choisir des années. En revanche, si vous souhaitez calculer la quantité de café restant dans votre corps après en avoir bu une tasse, l'unité de temps appropriée devrait être les heures ou peut-être les minutes.

Veuillez noter que $t$ ne doit pas nécessairement être considéré comme une unité de temps. Dans certains cas, la variable qui mesure le taux de variation peut être différente du temps. Par exemple, lorsque l'on étudie la manière dont la pression atmosphérique change avec l'altitude, la variable qui mesure ce changement est la distance, et vous devriez choisir les mètres comme unités de changement appropriées. Notre calculateur de pression atmosphérique en altitude 🇺🇸 peut vous aider dans ce cas.

La différence dans le taux de croissance exponentielle r aura une influence significative sur la vitesse à laquelle la quantité observée évolue par rapport à la valeur initiale. Partons de $x_0 = 100$ et, à l'aide du calculateur de croissance exponentielle, voyons ce que sera $x(10)$ pour quatre valeurs différentes de $r$ :

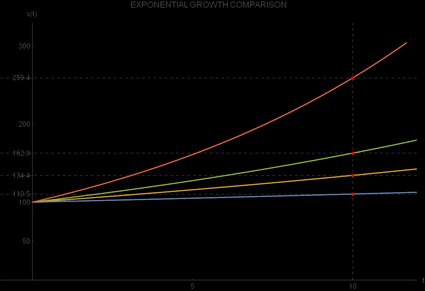
D'après ce tableau, nous constatons que toutes les valeurs initiales sont les mêmes, égales à $x_0 = 100$, mais que les valeurs finales de $x(10)$ diffèrent de manière significative. Votre intuition peut vous tromper ici, car la différence entre 1 % et 3 % ne semble pas énorme, mais après dix périodes, cela représente une valeur de $x(10)$ supérieure de 21,67 % pour une croissance de 3 % par rapport à une croissance de 1 %.

Si vous comparez la croissance de 10 % à celle de 5 %, vous remarquerez une différence encore plus grande, soit 59,23 % pour une croissance de 10 %. Vous pouvez observer ce contraste avec la représentation graphique des quatre fonctions de croissance exponentielle suivantes :

La formule de la croissance et de la décroissance exponentielle est utilisée pour modéliser divers phénomènes du monde réel :

• la croissance de la population de bactéries, de virus, de plantes, d'animaux et de personnes ;
• la décroissance des matières radioactives ;
• la concentration de médicaments dans le sang ;
• la pression atmosphérique de l'air à une certaine altitude ;
• les intérêts composés et la croissance économique ;
• la datation au radiocarbone ; et
• la puissance de traitement des ordinateurs, etc.

Comment les populations croissent : les équations exponentielles et logistiques

Deux modèles de croissance de la population

La population mondiale n'a pas connu de croissance exponentielle depuis au moins un demi-siècle

Croissance exponentielle de la population

Pharmacologie de la caféine

Effets de la caféine sur le sommeil si elle est prise 0,3 ou 6 heures avant d'aller au lit