Calculateur de coefficient binomial

Bienvenue sur le calculateur de coefficient binomial, où vous aurez l'occasion de calculer k parmi n et d'en apprendre plus sur cette mystérieuse formule. L'expression indique le nombre de combinaisons de k éléments d'un ensemble de n éléments et correspond à la touche nCr d'une calculatrice scientifique.

Poursuivez votre lecture pour comprendre la notion de binôme, la définition de la combinaison, et la différence entre permutation et combinaison. Intéressé·e ? Alors, foncez !

En mathématiques (en algèbre pour être précis), un binôme est un polynôme à deux termes (d'où le préfixe « bi‑ »). Par exemple, les expressions x + 1, xy - 2ab, ou x³z - 0,5y⁵ sont toutes des binômes, mais x⁵, a + b - cd, ou x² - 4x² ne le sont pas (la dernière expression a bien deux termes, mais on peut la simplifier en -3x², qui n'en a qu'un).

Maintenant que nous savons ce qu'est un binôme, regardons de plus près lorsqu'un binôme est élevé à une certaine puissance :

(x² - 3)³

Il existe des cas particuliers de cette expression. Par exemple, les identités remarquables que vous connaissez peut-être de l'école :

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

Le polynôme que nous obtenons du côté droit correspondant à la formule du binôme de Newton de ce que nous avions entre parenthèses. Croyez-le ou non, nous pouvons trouver leurs formules pour toute puissance entière positive. De manière générale, le théorème du binôme de Newton ressemble à ceci :

où :

• $C_k$ – le nombre de toutes les combinaisons possibles de $k$ éléments d'un ensemble de $n$ éléments

De plus, pour un n donné, ces nombres sont présentés de manière ordonnée pour des valeurs consécutives de n dans les lignes du célèbre triangle de Pascal, où une seule ligne entière compte tous les sous-ensembles possibles de l'ensemble (à savoir le cardinal de l'ensemble des parties). Visitez notre calculateur de triangle de Pascal 🇺🇸 pour générer un triangle de Pascal de la taille que vous souhaitez.

C'est enfin le bon moment pour en apprendre plus sur le concept de « combinaison ». Jetez un œil à la section ci-dessous.

Imaginez que vous êtes un·e étudiant·e à l'université, en train de faire une sieste pendant un cours magistral. Soudain, le professeur vous ramène à la réalité en disant : « Formons les groupes pour les projets de mi-semestre au hasard ! ».

Le problème est qu'il n'y a qu'un seul camarade avec qui vous aimeriez travailler sur le projet. Si le groupe compte vingt personnes et que le professeur vous divise en groupes de quatre, quelle est la probabilité que vous soyez avec votre ami ?

Chaque groupe possible est un exemple de combinaison. Dans ce cas, une combinaison de quatre éléments d'un ensemble de vingt éléments, ou, si vous préférez, de quatre étudiants d'un groupe de vingt personnes. Pour être un peu plus technique, choisir une combinaison signifie choisir un sous-ensemble d'un ensemble plus grand. Ce qui est important ici, c'est que l'ordre des éléments que nous choisissons n'a pas d'importance. Après tout, tous les membres d'une équipe de projet sont égaux.

Le nombre de combinaisons de k éléments d'un ensemble de n éléments se note tel que :

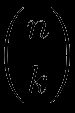
C'est un peu comme une fraction de n sur k mais sans la barre entre les deux. Nous lisons cette formule comme « k parmi n ». C'est aussi le symbole qui apparaît quand on tape sur nCr d'une calculatrice scientifique. Par exemple :

C'est « 2 parmi 4 ».

C'est « 2 parmi 6 ».

Dans certains manuels, le coefficient binomial est également désigné par C(n,k), ce qui en fait une fonction de n et k. Calculer C(n,k) est en réalité assez facile. La formule k parmi n est la suivante :

n! / (k ! × (n - k)!)

Le point d'exclamation est appelé factorielle. L'expression n! est le produit des n premiers nombres naturels, c'est-à-dire :

n! = 1 × 2 × 3 × ... × n

Cela signifie que l'expression 2 parmi 4 se calcule comme suit :

4! / (2! × (4 - 2)!) = (1 × 2 × 3 × 4) / (1 × 2 × 1 × 2) = 6

Et que 2 parmi 6 se calcule ainsi :

6! / (2! × (6 - 2)!) = (1 × 2 × 3 × 4 × 5 × 6) / (1 × 2 × 1 × 2 × 3 × 4) = 15

Pour en savoir plus sur les factorielles, visitez notre calculateur de factorielle !

On peut donc choisir deux éléments d'un ensemble de quatre éléments de six façons différentes, et d'un ensemble de six éléments, de quinze façons.

Avant de passer à autre chose, jetons un coup d'œil à la formule k parmi n. Nous pouvons en tirer une propriété symétrique très intéressante.

Si nous prenons n - k parmi n , alors nous avons :

n! / ((n - k)! × (n - (n - k))!) = n! / ((n - k)! × k!)

Ce qui est la même chose que k parmi n (puisque la multiplication est commutative). En d'autres termes, nous avons :

Ou C(n,k) = C(n,n-k) dans l'autre notation.

Dans la section ci-dessus, nous avons vu ce qu'est une factorielle. En combinatoire, elle indique le nombre de permutations. Une permutation de longueur n consiste à mettre n éléments dans un certain ordre. Par exemple, si nous avons trois expressions de chatons mignons, disons 😹, 😻, et 🙀, nous pouvons les ordonner de six façons différentes :

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹)

Observez que ceci est en accord avec ce que nous dit la factorielle :

3! = 3 × 2 × 1 = 6

Visitez notre calculateur de permutation 🇺🇸 pour plus de détails.

Notez que nous pouvons aussi comprendre cette formule comme ceci : nous choisissons le premier élément parmi trois éléments (3 options), le deuxième parmi les deux restants (parce que nous en avons déjà choisi un : 2 options), et le troisième parmi celui qui reste (puisque nous en avons déjà choisi deux : 1 option). On multiplie le nombre de choix : 3 × 2 × 1 = 6, et on obtient la factorielle.

Lorsque nous comparons la permutation à la combinaison, le mot-clé est : l'ordre. Comme nous l'avons dit dans la section précédente, la combinaison consiste à choisir un certain nombre d'éléments dans une collection plus grande. En substance, nous disons quels éléments nous choisissons, mais pas lequel est le premier, le deuxième, etc. Ils forment un ensemble en tant que tel.

Une permutation, en revanche, place les éléments dans un ordre fixe, l'un après l'autre, ce qui en fait une séquence plutôt qu'un ensemble. De plus, une permutation utilise tous les éléments de l'ensemble que nous avons eu, alors qu'une combinaison ne choisit que certains d'entre eux.

À titre d'exemple, mettez-vous à nouveau à la place de l'étudiant·e. Lorsque le professeur a choisi le groupe pour vous, il a choisi une combinaison. Et quand vient le moment de présenter votre projet, et qu'il pose une question à chacun d'entre vous, il choisit une permutation (déterminant l'ordre dans lequel il vous pose les questions).

Les coefficients binomiaux sont l'une des séquences de nombres les plus importantes en mathématiques discrètes et en combinatoire. Ils apparaissent très souvent dans les calculs de statistiques et de probabilités, et sont peut-être les plus importants dans la loi binomiale (y compris la loi binomiale négative 🇺🇸). Est-ce que cela veut dire qu'ils ne sont utiles qu'aux seuls mathématiciens ?

Pas du tout ! Tous les jeux de hasard sont basés sur les probabilités, et les coefficients binomiaux en sont l'acteur essentiel. Un simple jeu de pile ou face est l'exemple le plus simple, que vous pouvez calculer avec notre calculateur de pile ou face. Cependant, allons un peu plus loin et considérons le poker.

Vous êtes-vous déjà demandé pourquoi certaines mains au poker ont plus de valeur que d'autres ? C'est tout simplement parce qu'elles sont plus rares (à moins que quelqu'un ne triche, mais nous avons vu suffisamment de séries télévisées sur les gangsters pour savoir que c'est généralement une mauvaise idée).

Il y a 52 cartes dans un jeu de cartes normal, et au Texas hold 'em, un joueur reçoit cinq cartes. Notre calculateur de coefficient binomial et la formule k parmi n (dans notre cas avec n = 52 et k = 5) nous indique que cela se traduit par 2 598 960 mains possibles dans une partie de poker. C'est beaucoup, vous ne trouvez pas ? Considérons maintenant la meilleure main possible : une quinte royale à trèfle (As, Roi, Reine, Valet et 10). Cette main ne peut se produire que dans un seul cas : lorsque nous obtenons exactement ces cartes. On a donc 1 chance sur 2 598 960 de l'avoir. Nous vous déconseillons de miser toutes vos économies sur la probabilité d'avoir cette main.

Prenons un autre exemple : la probabilité d'avoir un full (un brelan et une paire). Cette fois-ci, il y a considérablement plus de possibilités. Après tout, n'importe laquelle des 13 cartes d'une couleur peut être le brelan, et la paire se trouve dans l'une des autres 12 cartes (elle ne peut pas être de la même valeur que le brelan). De plus, le brelan n'est présent que dans trois des quatre symboles de cartes, et de la même façon, la paire n'est présente que dans deux symboles.

Et c'est là que nous rappelons la définition d'une combinaison ! Nous devons choisir trois symboles parmi quatre pour le brelan et une combinaison de deux symboles parmi quatre pour la paire. La formule k parmi n traduit cela en 3 parmi 4 et 2 parmi 4, et le calculateur de coefficient binomial donne respectivement 4 et 6. En fin de compte, multiplions maintenant les nombres que nous avons obtenus :

13 × 12 × 4 × 6 = 3 744

Il y a 3 744 mains possibles qui donnent un full. Bon, ce n'est pas beaucoup par rapport à toutes les possibilités, mais au moins c'est 3 744 fois plus probable que la quinte royale à trèfle.

Quoi qu'il en soit, nous vous suggérons d'épargner régulièrement de l'argent, car c'est une meilleure technique d'investissement que le jeu de hasard.