Calculateur d'angle d'un triangle

Le calculateur d'angle d'un triangle est une valeur sûre si vous voulez savoir comment trouver l'angle d'un triangle. Que vous connaissiez les trois côtés d'un triangle, deux côtés et un angle ou seulement deux angles, cet outil est une solution à vos problèmes de géométrie. Vous trouverez également ci-dessous l'explication des lois fondamentales concernant les angles d'un triangle : le théorème de la somme des angles d'un triangle, le théorème de l'angle extérieur d'un triangle et le théorème de la bissectrice de l'angle. Lisez la suite pour comprendre comment le calculateur fonctionne, et essayez-le ! Vous verrez, trouver les angles manquants des triangles n'aura jamais été aussi facile !

Il existe plusieurs façons de trouver les angles d'un triangle, en fonction des données que nous avons :

1. Les trois côtés d'un triangle sont donnés 

Utilisez les formules transformées de la loi des cosinus:

Ainsi :

Pour le deuxième angle, nous avons :

Ainsi :

Et enfin, pour le troisième angle :

Ainsi :

2. Deux côtés d'un triangle et un angle sont donnés 

Si l'angle est entre les côtés donnés, vous pouvez directement utiliser la loi des cosinus pour trouver le troisième côté inconnu, puis utiliser les formules ci-dessus pour trouver les angles manquants, en connaissant a,b,γ.

• Calculez :

  $c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$

• Remplacez $c$ par :

  $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$

• Puis trouvez $\beta$ à partir du théorème de la somme des angles d'un triangle :

  $\beta = 180\degree- \alpha - \gamma$

Si l'angle n'est pas entre les côtés donnés, vous pouvez utiliser la loi des sinus. Par exemple, supposons que vous connaissiez $a$, $b$, et $\alpha$:

Ainsi :

• Comme vous le savez, la somme des angles d'un triangle est égale à $180\degree$. Ce théorème nous permet de trouver l'angle manquant :

  $\gamma = 180\degree- \alpha - \beta$

3. Deux angles sont donnés

C'est l'option la plus simple. Il suffit d'utiliser le théorème de la somme des angles d'un triangle pour trouver l'angle manquant :

• $\alpha = 180\degree- \beta - \gamma$
• $\beta= 180\degree- \alpha - \gamma$
• $\gamma = 180\degree- \alpha- \beta$

Dans les trois cas, vous pouvez utiliser notre calculateur d'angle d'un triangle, il vous sera forcément utile.

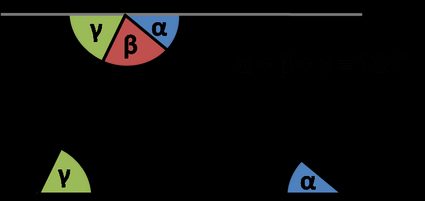
Le théorème stipule que la somme des angles intérieurs d'un triangle est égale à $180\degree$ :

Mais comment le savons-nous ? Regardez l'image : les angles désignés par les mêmes lettres grecques sont congruents parce qu'il s'agit d'angles intérieurs alternés. La somme des trois angles $\alpha$,$\beta$ , $\gamma$ est égale à $180\degree$, car ils forment une droite ! C'est pourquoi $\alpha + \beta+ \gamma = 180\degree$.

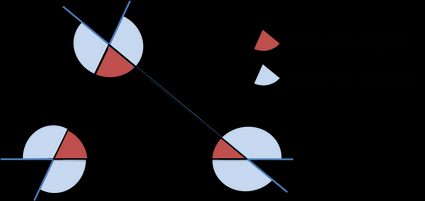
L'angle extérieur d'un triangle est égal à la somme des angles intérieurs opposés.

• Chaque triangle a six angles extérieurs. (Les deux situés au même sommet sont égaux.)
• Les angles extérieurs, pris un à chaque sommet, font toujours $360\degree$.
• Un angle extérieur est complémentaire de l'angle intérieur du triangle qui lui est adjacent.

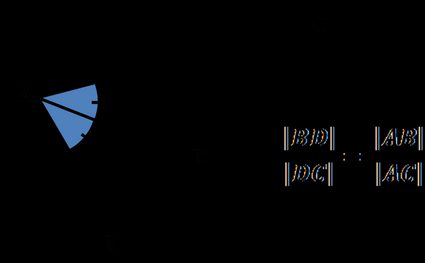
Le théorème de la bissectrice indique que la bissectrice d'un angle d'un triangle divise le côté opposé en deux segments proportionnels aux deux autres côtés du triangle.

Ou, en d'autres termes :

Le rapport entre la longueur de $\overline{BD}$ et la longueur de $\overline{DC}$ est égal au rapport entre la longueur du côté $\overline{AB}$ et la longueur du côté $\overline{AC}$ :

Mettons en pratique ce que nous venons de lire. Supposons que nous voulions trouver les angles manquants dans notre triangle. Comment procéder ?

1. Trouvez les formules que vous devez utiliser. Dans notre exemple, nous avons deux côtés et un angle. Choisissez l'option angle et 2 côtés.
2. Saisissez les valeurs données. Par exemple, vous savez que $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$, et $\alpha = 30\degree$. Si vous voulez le calculer à la main, utilisez la loi des sinus :

Ainsi :

• D'après le théorème de la somme des angles dans un triangle, on trouve que :

  $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51,\!06\degree= 98,\!94\degree$

3. Le calculateur d'angle d'un triangle trouve les angles manquants dans le triangle. Ils sont égaux à ceux que nous avons calculés à main :

   $\beta = 51,\!06\degree$ et $\gamma = 98,\!94\degree$

   De plus, l'outil a déterminé la dernière longueur de côté :

   $c = 17,\!78\ \mathrm{cm}$

Des raisonnements similaires à ceux que nous avons appliqués dans ce calculateur apparaissent dans d'autres calculs de triangles, par exemple ceux que nous utilisons dans le calculateur de triangle ACA 🇺🇸 et le calculateur de triangle CCA 🇺🇸 !