Calcul d'arctan (tan⁻¹) | Outil en ligne

Q: À quoi est égal arctan(x) ?

L' arctan(x) est égale à la fonction tangente inverse : tan⁻¹(x) . Si dans un triangle rectangle, le tan de l'angle détermine le rapport de la perpendiculaire à la base ( tan(x) = perpendiculaire / base ), alors l'arctan nous aidera à trouver la valeur de l'angle x : x = tan⁻¹(perpendiculaire / base) .

Q: Est-ce qu'arctan est la même chose que tan⁻¹ ?

Oui , arctan est la même chose que tan⁻¹ et signifie la fonction tangente inverse. Cependant, soyez prudent·e pour ne pas confondre tan-¹(x) avec (tan(x))-¹ , qui signifie 1/tan(x) et fait référence à l'autre fonction trigonométrique, la cotangente de x .

Q: Qu'est-ce qu'arctan(1) ?

Arctan(1) (ou tan⁻¹(1) ) donne la mesure de l'angle d'un triangle rectangle dans lequel le rapport du côté opposé et du côté adjacent à l'angle est égal à 1 . La valeur d'arctan 1 est 45° ou π/4 radians .

Q: Qu'est-ce qu'arctan(√3) ?

La valeur exacte de arctan(√3) est 60° ou π/3 . Puisque tan(60°) = √3 et que arctan est la fonction inverse de tan, arctan(√3) sera 60°.

Q: Comment dessiner le graphique d'arctan ?

Pour dessiner le graphique de l'arctan et lire les valeurs pour certains angles : Dessinez un système de coordonnées , où l'axe des y est l'axe horizontal, et l'axe des x est l'axe vertical. Dessinez le graphique de x = tan(y) mais seulement dans l'intervalle <-π/2;π/2> . Faites pivoter le graphique de 90 degrés dans le sens des aiguilles d'une montre . Vous avez trouvé ! Voici, le graphique de y = arctan(x) .

Q: Quelle est l'intégrale de l'arctan ?

Puisque arctan(x) = tan⁻¹(x) , l'intégrale d'arctan est l'intégration de l'inverse de tan x, que l'on peut écrire mathématiquement comme suit : ∫tan⁻¹(x) dx = x tan⁻¹(x) - ½ ln |1+x²| + C Dans cette équation, C est la constante d'intégration, dx indique que l'intégration de l'inverse de tan x se fait par rapport à x, et ∫ indique le symbole d'intégration.

Q: Quelle est la dérivée d'arctan ?

La dérivée de la fonction arctan est : d/dx(arctan(x)) = 1/(1+x²) . La fonction arctan peut être dérivée car sa dérivée existe en tout point de son domaine. En observant le graphique de la période unique de la fonction arctan(x), vous remarquerez que la courbe est continue .

Créateurs

Hanna Pamuła, Docteur·e

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Traducteurs

Claudia Herambourg

Claudia Herambourg is an aspiring computational linguist with a passion for both words and numbers. She holds a Bachelor’s degree in English Literature and Mathematical Studies from University College Cork, Ireland. She is currently pursuing her Master’s degree in Linguistics at Sorbonne Nouvelle University in Paris, specializing in computational linguistics. In her spare time, you'll probably find her reading a book of Japanese literature that nobody has ever heard of, on a train going nowhere. See full profile

Check our editorial policy

Réviseurs

Bogna Szyk et Jack Bowater

Utilisez cet outil de calcul d'arctan (tan^-1) pour trouver rapidement l'inverse de la tangente. Que vous cherchiez une réponse simple à la question « qu'est-ce qu'arctan ? » ou que vous soyez curieux ou curieuse de connaître l'intégrale ou la dérivée d'arctan, vous êtes au bon endroit. Vous trouverez également ci-dessous le graphique d'arctan, ainsi qu'un tableau reprenant les valeurs les plus couramment utilisées, telles qu'arctan(1) ou tan^-1(1) et arctan(0) ou tan⁰. Vous pouvez également taper la valeur qui vous intéresse dans cet outil et vous trouverez la réponse en un clin d'œil.

Vous êtes intéressé·e par des notions de trigonométrie plus avancées ? Consultez nos calculateurs loi des sinus 🇺🇸 et loi des cosinus 🇺🇸 si vous avez des triangles à résoudre.

Calcul d'arctan : qu'est-ce qu'arctan ?

La fonction « arctan » est l'inverse de la fonction tangente. Pour une analyse approfondie de la fonction tangente, consultez notre calculateur de tangente 🇺🇸. En termes simples, nous utilisons arctan lorsque nous voulons trouver un angle pour lequel nous connaissons la valeur de la tangente.

Cependant, au sens strict, la tangente étant une fonction trigonométrique périodique, elle n'a pas de fonction inverse. Néanmoins, nous pouvons définir une fonction inverse si nous restreignons le domaine à l'intervalle où la fonction est monotone. L'intervalle couramment choisi, $-\frac{\pi}{2}<y<\frac{\pi}{2}$ , est appelé mesure principale et constitue en même temps le domaine d'une fonction tangente inverse.

Abréviation	Définition	Domaine	Intervalle habituel de la mesure principale
$\text{arctan}(x)$
$\text{tan}^{-1}(x)$	$x = \tan(y)$	Nombres réels $\mathbb{R}$	$-\frac{\pi}{2}<y<\frac{\pi}{2}$ $-90\degree<y<90\degree$
$\text{atan}(x)$

L'utilisation de la convention $\tan^{-1}(x)$ peut prêter à confusion quant à la différence entre l'arc tangente et la cotangente. Il s'avère que l'arctan et le cot sont deux choses distinctes :

$\cot(x) = 1/\tan(x)$ la cotangente est donc l'inverse de la tangente ou, en d'autres termes, l'inverse multiplicatif ;
$\arctan(x)$ est l'angle dont la tangente est $x$ .

Nous espérons que vous n'avez plus aucun doute sur la différence entre l'arctan et la cotan. Pour éviter tout autre malentendu, vous pouvez utiliser la notation $\arctan(x)$ plutôt que $\tan^{-1}(x)$ .

🙋 Essayez maintenant le calculateur d'Omni si vous voulez apprendre à calculer toutes les fonctions trigonométriques 🇺🇸 !

Graphique d'arctan

En restreignant le domaine de la fonction tangente principale, nous obtenons la tangente inverse qui s'étend de $-\frac{\pi}{2}<y<\frac{\pi}{2}$ radians exclusivement. Cependant, le domaine d'une fonction arctangente est constitué de tous les nombres réels. Le graphique se présente alors comme suit :

$\boldsymbol{x}$	$\boldsymbol{\arctan(x)}$
	rad	deg
$-\infty$	$-\pi/2$	$-90\degree$
$-3$	$-1,\!2490$	$-71,\!565\degree$
$-2$	$-1,\!1071$	$-63,\!435\degree$
$-\sqrt 3$	$-\pi/3$	$-60\degree$
$-1$	$-\pi/4$	$-45\degree$
$-\sqrt{3}/3$	$-\pi/6$	$-30\degree$
$0$	$0$	$0$
$\sqrt{3}/3$	$\pi/6$	$30\degree$
$1$	$\pi/4$	$45\degree$
$\sqrt 3$	$\pi/3$	$60\degree$
$2$	$1,\!1071$	$63,\!435\degree$
$3$	$1,\!2490$	$71,\!565\degree$
$\infty$	$\pi/2$	$90\degree$

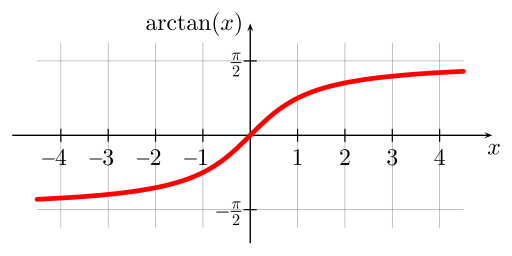
Comment le graphique de l'arctan est-il créé ? En faisant passer les $\tan(x)$ de l'intervalle $(-\pi/2, \pi/2)$ par la droite $y = x$ . Vous pouvez également le voir comme le fait d'intervertir les axes horizontaux et verticaux :

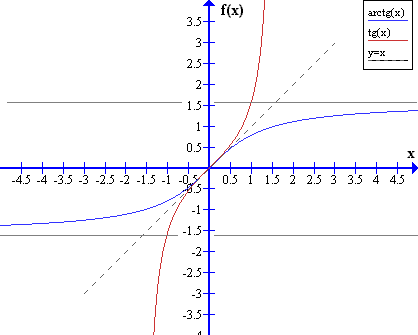
Propriétés de l'arctan, relations avec les fonctions trigonométriques, intégrale et dérivée de l'arctan

Les relations en trigonométrie sont cruciales pour comprendre ce sujet encore plus en profondeur. L'inspection du triangle rectangle dont les longueurs des côtés sont $1$ et $x$ est un bon point de départ si vous voulez trouver les relations entre arctan et les fonctions trigonométriques de base :

Sinus : $\sin(\arctan(x)) = x / \sqrt{1 + x^2}$
Cosinus : $\cos(\arctan(x)) = 1 / \sqrt{1 + x^2}$
Tangente : $\tan(\arctan(x)) = x$

D'autres relations utiles avec l'arc tangente sont :

$\arctan(x) = \pi/2 -\text{arccot}(x)$
$\arctan(-x) = -\arctan(x)$
$\arcsin(x) = \arctan\left(x / \sqrt{1 - x^2}\right)$ (rendez-vous au calculateur d'arcsin !)
Intégrale de l'arctan :

\begin{split} &\int\arctan(x) \text{d}x\\ & \!=\! x \arctan(x)\! -\! \frac{1}{2}\ln(1 \!+\! x^2) \!+ \!C \end{split}

Dérivée de l'arctan :

\frac{\text{d}}{\text{d}x}\! \arctan(x) \! =\! \frac{1}{1 \!+\! x^2}\ \text{if}\ x\! \neq\! \pm\text{i}

$\arctan(x) + \arctan(1/x) = \pi/2$ pour $x > 0$ et $\arctan(x) + \arctan(1/x) = -\pi/2$ , pour $x < 0$

Il est facile de prouver la première équation à partir des propriétés du triangle rectangle dont les longueurs des côtés sont $1$ et $x$ , car nous savons parfaitement que la somme des angles d'un triangle est égale à $180\degree$ . En soustrayant l'angle droit, qui est $90\degree$ , il nous reste deux angles non droits, dont la somme doit être égale à $90\degree$ . Nous pouvons donc écrire les angles sous la forme $\arctan(x)$ et $\arctan(1/x)$ .

Comment utiliser l'outil de calcul d'arctan

C'est l'un de nos calculateurs les plus faciles à utiliser, vraiment ! Il vous suffit d'entrer le nombre dont vous voulez trouver l'arctan. Comme le domaine de l'arctan est constitué de tous les nombres réels, vous n'avez pas à vous inquiéter outre mesure. Supposons que nous voulions trouver l'arctan de 1. Entrez simplement le nombre et le calculateur de tangente inverse affichera le résultat. Comme nous nous y attendions, l'arctan de 1 est égal à $45\degree$ . Cette calculatrice d'arctan fonctionne également dans l'autre sens, c'est-à-dire comme un calculateur de tangente standard - tapez l'angle dans la deuxième case et la tangente de cet angle s'affichera.

FAQ

À quoi est égal arctan(x) ?

L'arctan(x) est égale à la fonction tangente inverse : tan⁻¹(x). Si dans un triangle rectangle, le tan de l'angle détermine le rapport de la perpendiculaire à la base (tan(x) = perpendiculaire / base), alors l'arctan nous aidera à trouver la valeur de l'angle x : x = tan⁻¹(perpendiculaire / base).

Est-ce qu'arctan est la même chose que tan⁻¹ ?

Oui, arctan est la même chose que tan⁻¹ et signifie la fonction tangente inverse. Cependant, soyez prudent·e pour ne pas confondre tan-¹(x) avec (tan(x))-¹, qui signifie 1/tan(x) et fait référence à l'autre fonction trigonométrique, la cotangente de x.

Qu'est-ce qu'arctan(1) ?

Arctan(1) (ou tan⁻¹(1)) donne la mesure de l'angle d'un triangle rectangle dans lequel le rapport du côté opposé et du côté adjacent à l'angle est égal à 1. La valeur d'arctan 1 est 45° ou π/4 radians.

Qu'est-ce qu'arctan(√3) ?

La valeur exacte de arctan(√3) est 60° ou π/3. Puisque tan(60°) = √3 et que arctan est la fonction inverse de tan, arctan(√3) sera 60°.

Comment dessiner le graphique d'arctan ?

Pour dessiner le graphique de l'arctan et lire les valeurs pour certains angles :

Dessinez un système de coordonnées, où l'axe des y est l'axe horizontal, et l'axe des x est l'axe vertical.
Dessinez le graphique de x = tan(y) mais seulement dans l'intervalle <-π/2;π/2>.
Faites pivoter le graphique de 90 degrés dans le sens des aiguilles d'une montre.
Vous avez trouvé ! Voici, le graphique de y = arctan(x).

Quelle est l'intégrale de l'arctan ?

Puisque arctan(x) = tan⁻¹(x), l'intégrale d'arctan est l'intégration de l'inverse de tan x, que l'on peut écrire mathématiquement comme suit :

∫tan⁻¹(x) dx = x tan⁻¹(x) - ½ ln |1+x²| + C

Dans cette équation, C est la constante d'intégration, dx indique que l'intégration de l'inverse de tan x se fait par rapport à x, et ∫ indique le symbole d'intégration.

Quelle est la dérivée d'arctan ?

La dérivée de la fonction arctan est : d/dx(arctan(x)) = 1/(1+x²). La fonction arctan peut être dérivée car sa dérivée existe en tout point de son domaine. En observant le graphique de la période unique de la fonction arctan(x), vous remarquerez que la courbe est continue.