Logo d'Omni Calculator
Board

Calculateur de volume d'une cuve

Avec notre calculateur de volume d'une cuve, d'un réservoir, d'une citerne, vous pouvez facilement estimer le volume de votre conteneur. Choisissez parmi dix formes de cuves : des réservoirs rectangulaires et cylindriques standard aux réservoirs en forme de capsule et d'ellipse. Vous pouvez même trouver le volume du tronc d'un cône dans les réservoirs à fond conique. Il vous suffit d'entrer les dimensions de votre conteneur, et cet outil calculera pour vous le volume total du réservoir. Vous pouvez également indiquer la hauteur de remplissage, qui sera utilisée pour trouver le volume rempli.

Vous vous demandez comment il marche ? Faites défiler la page et vous trouverez toutes les formules dont vous avez besoin : le volume d'une cuve rectangulaire, d'un réservoir elliptique ou de réservoir à fond conique très répandus, ainsi que beaucoup d'autres !

Vous recherchez d'autres types de réservoirs ou cuves, de formes différentes et pour d'autres applications ? Consultez notre calculateur de volume pour trouver le volume des solides tridimensionnels les plus courants. Pour un usage plus spécialisé, vous pouvez aussi jeter un coup d'œil au calculateur d'aquarium et au calculateur de piscine pour trouver des solutions à des problèmes de volume quotidiens.

Comment utiliser le calculateur de volume d'une cuve ?

Ce calculateur de volume d'une cuve est un outil simple qui vous aide à trouver le volume d'un réservoir ou d'une cuve ainsi que le volume de la partie remplie. Vous avez le choix entre dix formes de réservoirs :

  • Cylindre vertical
  • Cylindre horizontal
  • Prisme rectangulaire (parallélépipède rectangle, pavé droit)
  • Capsule verticale
  • Capsule horizontale
  • Ovale vertical (elliptique)
  • Ovale horizontal (elliptique)
  • Fond conique
  • Sommet conique
  • Tronc de cône

Mais comment utiliser ce calculateur de volume d'une cuve ? Prenons un exemple simple :

  1. Décidez de la forme. Supposons que nous voulions calculer le volume d'une cuve à cylindre vertical : choisissez cette option dans la liste déroulante. L'image schématique du réservoir apparaîtra ci-dessous ; assurez-vous que c'est bien celle que vous voulez !

  2. Saisissez les dimensions de la cuve ou du réservoir. Dans notre cas, nous devons saisir la longueur et le diamètre. Dans notre exemple, ils sont respectivement égaux à 32 cm32\ \mathrm{cm} et 24 cm24\ \mathrm{cm}. En outre, nous pouvons saisir la hauteur de remplissage : 28 cm28\ \mathrm{cm}.

  3. Le calculateur de volume d'une cuve a déjà trouvé le volume total et le volume rempli Le volume total du réservoir est 883 cm3883\ \mathrm{cm^3}, et le volume du liquide à l'intérieur est 773 cm3773\ \mathrm{cm^3}. Comme toujours, vous pouvez modifier les unités en cliquant sur les unités de volume elles-mêmes. C'est simple comme bonjour !

Formule de calcul du volume d'une cuve cylindrique

Pour calculer le volume total d'une cuve cylindrique, il suffit de connaître le diamètre du cylindre (ou rayon) et sa hauteur (que l'on peut appeler longueur s'il est placé à l'horizontale).

Cuve cylindrique verticale

Réservoir cylindrique vertical avec dimensions.

Nous pouvons trouver le volume total d'un réservoir cylindrique à l'aide de la formule standard du volume : l'aire de la base multipliée par la hauteur. Un cercle étant la forme de la base, sa surface, selon l'équation bien connue, est égale à π×rayon2\pi \times \mathrm{rayon}^2. Par conséquent, la formule pour le volume d'un réservoir cylindrique vertical est la suivante :

Vcylindre vertical=π×r2×h=π×(d2)2×h\begin{split} V_{\scriptsize{\mathrm{\tiny cylindre\ vertical}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h \end{split}

où :

  • rr – rayon de la base
  • hh  – hauteur du cylindre

Si nous voulons calculer le volume rempli, nous devons trouver le volume d'un cylindre « plus petit » ; c'est aussi simple que cela !

Vcylindre vertical=π×r2×h=π×(d2)2×h\begin{split} V_{\scriptsize{\mathrm{\tiny cylindre\ vertical}}} &= \pi \times r^2 \times h\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times h \end{split}

où ff est la hauteur de la partie remplie du cylindre.

Cuve cylindrique horizontale

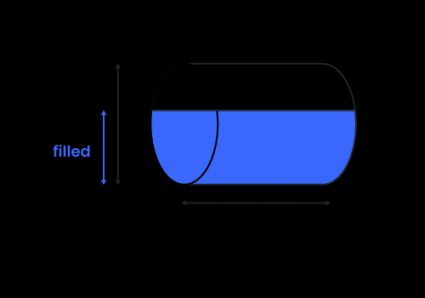
Réservoir cylindrique horizontal avec dimensions.

Le volume total d'une cuve cylindrique horizontale peut être calculé de manière analogue : il s'agit de l'aire de l'extrémité circulaire multipliée par la longueur du cylindre :

Vcylindre horizontal=π×r2×L=π×(d2)2×L\begin{split} V_{\scriptsize{\mathrm{\tiny cylindre\ horizontal}}} &= \pi \times r^2 \times L\\[.6em] &=\pi\times\left(\frac{d}{2}\right)^2\times L \end{split}

où LL est la longueur du cylindre.

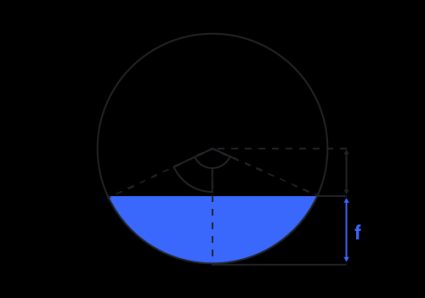
Coupe transversale d'un réservoir cylindrique partiellement rempli.

Les choses se compliquent lorsque nous voulons trouver le volume du cylindre horizontal partiellement rempli. Tout d'abord, nous devons trouver l'aire de base, c'est-à-dire l'aire du segment circulaire couvert par le liquide :

Asegment=12×r2×(θ−sin⁡(θ))A_{\mathrm{\tiny segment}} = \frac{1}{2}\times r^2 \times (\theta-\sin(\theta))

où rr est le rayon de la base et θ\theta est l'angle central du segment. L'angle θ\theta peut être calculé à l'aide de la formule du cosinus :

cos⁡(θ2)=r−ff\cos\left(\frac{\theta}{2}\right) = \frac{r-f}{f}

où ff est la hauteur de la section remplie de la base.

Ainsi :

θ=2×cos⁡−1(r−ff)\theta= 2\times \cos{^-1}\left(\frac{r-f}{f}\right)

Enfin, la formule pour le volume d'un cylindre horizontal partiellement rempli VfhcV_{\scriptsize{\mathrm{fhc}}} est la suivante :

Vfhc=0, ⁣5×r2×(θ−sin⁡(θ))×L\small V_{\scriptsize{\mathrm{fhc}}} = 0,\!5\times r^2\times(\theta -\sin(\theta))\times L

où :

θ=2×cos⁡−1(r−fr)\theta = 2\times \cos^{-1}\left(\frac{r-f}{r}\right)

Si le cylindre est plus qu'à moitié pleine, il est plus facile de soustraire la partie vide du réservoir du volume total.

Calculateur de volume d'une cuve rectangulaire (prisme rectangulaire)

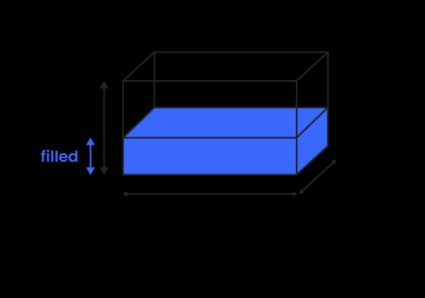
Réservoir rectangulaire aux dimensions indiquées.

Si vous vous demandez comment calculer le volume d'une cuve rectangulaire (également appelé parallélépipède rectangle, pavé droit), ne cherchez pas plus loin ! Vous connaissez peut-être ce réservoir sous le nom de réservoir rectangulaire ;mais ce n'est pas son nom exact, car un rectangle est une forme 2D, et il n'a donc pas de volume.

Pour trouver le volume du prisme rectangulaire, multipliez toutes les dimensions du réservoir :

Vpaveˊ droit=h×l×LV_{{\mathrm{pavé\ droit}}} = h\times l\times L

où :

  • hh  – la hauteur du réservoir
  • ll – la largeur
  • LL – la longueur du réservoir

Si vous souhaitez connaître le volume du liquide contenu dans un réservoir, il vous suffit de remplacer la variable hauteur par rempli dans la formule du volume d'un réservoir rectangulaire. Le volume d'un prisme rectangulaire rempli, VrpdV_{\scriptsize{\mathrm{rpd}}} , est :

Vrpd=f×l×LV_{{\mathrm{rpd}}} = f\times l\times L

où ff est la hauteur de la partie remplie.

Pour ce calculateur de volume d'une cuve, peu importe que le réservoir soit en position horizontale ou verticale. Assurez-vous simplement que rempli et hauteur sont sur le même axe.

Formule pour le volume d'une capsule

Notre outil définit une capsule comme deux hémisphères séparés par un cylindre. Pour calculer le volume total d'une capsule, il suffit d'ajouter le volume de la sphère à celui du cylindre :

Vcapsule=π ⁣× ⁣ ⁣(d2)2 ⁣ ⁣ ⁣× ⁣(43 ⁣× ⁣d2 ⁣+ ⁣L)V_{\scriptsize{\mathrm{capsule}}} = \pi\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\!\times\!\left(\frac{4}{3}\!\times\!\frac{d}{2}\!+\!L\right)

Selon la position du réservoir, les calculs du volume rempli diffèrent quelque peu :

1. Pour une cuve à capsule horizontale

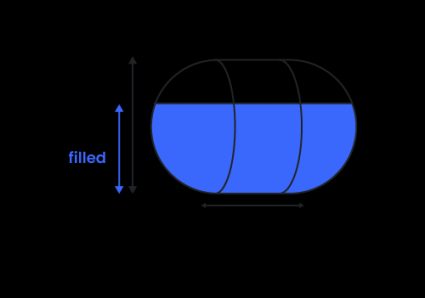
Réservoir à capsule horizontale avec dimensions indiquées.

Comme les hémisphères situés à chaque extrémité du réservoir sont identiques, ils forment une calotte sphérique : ajoutez cette partie Vsph hfV_{\scriptsize{\mathrm{sph\ hf}}} à la partie du cylindre horizontal VfhcV_{\scriptsize{\mathrm{fhc}}} (vérifiez le paragraphe ci-dessus) pour calculer le volume du liquide dans une capsule horizontale remplie (Vcap hfV_{\scriptsize{\mathrm{cap\ hf}}}) :

Vcap hf=Vfhc+Vsph hf=12 ⁣× ⁣ ⁣(d2)2 ⁣ ⁣ ⁣× ⁣(θ−sin⁡(θ))×L+π×f23 ⁣× ⁣(32×d−f)\begin{split} &V_{\scriptsize{\mathrm{cap\ hf}}} = V_{\scriptsize{\mathrm{fhc}}}+V_{\scriptsize{\mathrm{sph\ hf}}}\\[.6em] &= \frac{1}{2}\!\times\!\! \left(\frac{d}{2}\right)^2\!\!\! \times\! (\theta-\sin(\theta))\times L \\[1em] &\quad+\frac{\pi\times f^2}{3}\!\times\!\left(\frac{3}{2}\times d-f\right) \end{split}

où :

  • dd – le diamètre du réservoir
  • ff – la hauteur de remplissage
  • θ\theta – l'angle correspondant au secteur rempli dans le réservoir cylindrique

2. Pour les cuves à capsule verticale

La formule diffère pour différentes hauteurs de remplissage. Dans toutes les formules suivantes, nous rencontrerons ces quantités :

  • dd – le diamètre du réservoir

  • ff – la hauteur atteinte par le liquide

  • LL – la longueur de la section cylindrique

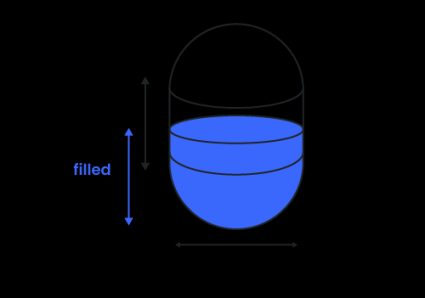
Réservoir à capsule verticale avec dimensions indiquées.
  • Si f<d/2f < d/2, le liquide ne se trouve que dans la partie inférieure de l'hémisphère, nous n'avons donc besoin que de la formule du volume d'une calotte sphérique :
Vcap f=(π ⁣× ⁣f)23 ⁣× ⁣(32 ⁣× ⁣d−f)\\[2em] V_{\scriptsize{\mathrm{cap\ f}}} = \frac{(\pi\!\times \!f)^2}{3}\!\times\!\left(\frac{3}{2}\!\times \!d - f\right) \\[2em]
  • Si d/2<f<d/2+Ld/2 < f < d/2 +L, nous devons ajouter le volume de l'hémisphère et le cylindre « plus petit » :
   Vcap f=23×π(d2)3+π×(d2)2×f−d2\quad\ \ \ \begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = \frac{2}{3}\times \pi\left(\frac{d}{2}\right)^3\\[1em] &\qquad+\pi\times\left(\frac{d}{2}\right)^2\times\frac{f-d}{2} \end{split}
  • Si d/2+L<fd/2 + L < f, cela signifie que l'hémisphère inférieur et le cylindre sont pleins. Il suffit donc de soustraire la calotte sphérique (partie vide) du volume total :
Vcap f=Vcap ⁣− ⁣π×(L+d−f)23  ×(32×d−(L+d−f))\begin{split} &V_{\scriptsize{\mathrm{cap\ f}}} = V_{\scriptsize{\mathrm{cap}}}\! -\! \frac{\pi\times(L+d-f)^2}{3}\\ &\qquad\ \ \times\left(\frac{3}{2}\times d - (L+d-f)\right) \end{split}

Volume d'une cuve elliptique (réservoir ovale)

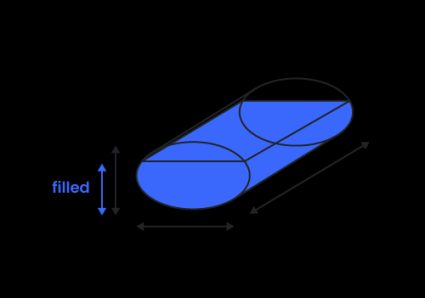
Réservoir ovale horizontal aux dimensions indiquées.

Dans notre calculateur de volume d'une cuve, nous définissons un réservoir ovale comme un réservoir cylindrique avec une extrémité elliptique (et non en forme de stade, comme il est parfois défini). Pour trouver le volume total d'un réservoir elliptique, vous devez multiplier la surface de l'ellipse par la longueur du réservoir :

Vellipse=π ⁣× ⁣l ⁣× ⁣L ⁣× ⁣h4V_{\scriptsize{\mathrm{ellipse}}} = \pi\!\times\!l\!\times\!L\!\times\!\frac{h}{4}

où :

  • ll – largeur du réservoir
  • hh – hauteur de la citerne
  • LL –longueur de la citerne
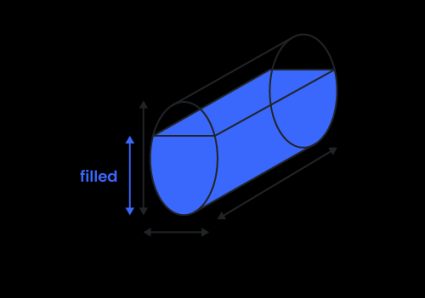
Réservoir ovale vertical aux dimensions indiquées.

Enfin une autre formule facile ! Malheureusement, il n'est pas aussi simple de trouver le volume d'un réservoir partiellement rempli, que ce soit à l'horizontale ou à la verticale. Vous devez utiliser la formule de l'aire du segment d'ellipse et multiplier le résultat par la longueur du réservoir :

Vell f=L ⁣× ⁣h ⁣× ⁣w4× ⁣[cos⁡−1(1 ⁣− ⁣2 ⁣× ⁣fh) ⁣ ⁣− ⁣( ⁣1 ⁣− ⁣2 ⁣× ⁣fh ⁣) ⁣× ⁣4 ⁣× ⁣fh ⁣− ⁣4 ⁣× ⁣f2h2]\begin{split} &V_{\scriptsize{\mathrm{ell\ f}}} = L\!\times\!h\!\times\!\frac{w}{4}\\[1em] &\qquad\times\!\left[\cos^{-1}\left(1\!-\!\frac{2\!\times\!f}{h}\right)\right.\\[1.5em] &\!\!\left.-\!\left(\!1\!-\!\frac{2\!\times\!f}{h}\!\right)\!\times\!\sqrt{\frac{4\!\times\!f}{h}\!-\!\frac{4\!\times\!f^2}{h^2}}\right] \end{split}

Volume d'un tronc de cône (cuve en forme de cône tronqué)

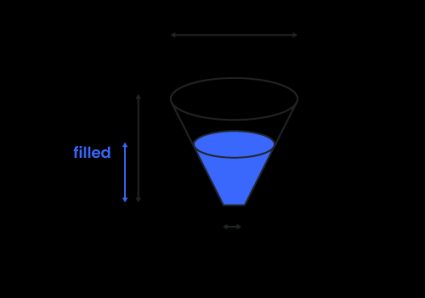
Réservoir tronc de cône avec dimensions indiquées.

Pour calculer le volume d'un cône tronqué (une forme particulière rencontrée lors de notre calculateur de cône tronqué 🇺🇸), utilisez la formule suivante :

Vtronc=13×π×hco^ne×((dsup2)2 ⁣+ ⁣dsup2 ⁣× ⁣dinf2 ⁣+ ⁣(dinf2)2)\begin{split} &V_{\scriptsize{\mathrm{tronc}}} = \frac{1}{3}\times\pi\times h_{\mathrm{cône}}\\[1em] &\qquad\times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\!+\! \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!\right.\\[1em] &\qquad\qquad \left.+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

où :

  • dsupd_{\mathrm{sup}} – diamètre supérieur du tronc de cône
  • dinfd_{\mathrm{inf}} – diamètre inférieur du tronc de cône
  • hco^neh_{\mathrm{cône}} – hauteur de la cuve
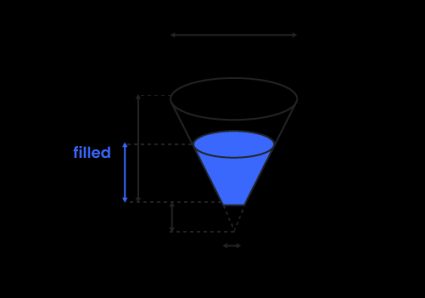
Réservoir tronc de cône avec dimensions et niveau de liquide indiqués.

Si vous souhaitez connaître le volume du tronc de cône partiellement rempli pour une hauteur de remplissage donnée, calculez d'abord le rayon supérieur de la partie remplie :

R=12×dsup×f+zhco^ne+zR = \frac{1}{2} \times d_{\mathrm{sup}}\times \frac{f+z}{h_{\mathrm{cône}}+z}

où :

z=hcone×dinfdsup−dinfz = h_\mathrm{cone} \times \frac{d_{\mathrm{inf}}}{d_{\mathrm{sup}}-d_{\mathrm{inf}}}

(Vous pouvez dériver la formule à partir de la similitude des triangles)

Ensuite, il suffit de trouver le nouveau volume du tronc de cône :

Vff=13×π×f  × ⁣(R2 ⁣+ ⁣R ⁣× ⁣dinf2+(dinf2)2)\begin{split} &V_{\scriptsize{\mathrm{ff}}}=\frac{1}{3} \times \pi \times f \\ &\ \ \times \!\left(R^2 \!+ \!R\! \times \!\frac{d_{\mathrm{inf}}}{2} + \left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right) \end{split}

Volume des cuves à fond conique (réservoir conique) et des cuves à sommet conique

Réservoir à fond conique avec dimensions indiquées.

Trouver le volume total d'un réservoir à fond conique n'est pas si difficile : il suffit d'ajouter le volume de la partie du tronc au volume de la partie cylindrique :

Vco^ne b=Vtronc+Vcylindre=13×π×hco^ne×((dsup2)2+dsup2 ⁣× ⁣dinf2 ⁣+ ⁣(dinf2)2)+π×(dsup2)2×hcylindre\begin{split} &V_{\scriptsize{\mathrm{cône\ b}}} = V_{\scriptsize{\mathrm{tronc}}} + V_{\scriptsize{\mathrm{cylindre}}}\\[1em] & =\frac{1}{3}\times\pi\times h_{\mathrm{cône}} \times\left( \left(\frac{d_{\mathrm{sup}}}{2}\right)^2\right.\\[1.4em] &\qquad \left.+ \frac{d_{\mathrm{sup}}}{2}\!\times\!\frac{d_{\mathrm{inf}}}{2}\!+\!\left(\frac{d_{\mathrm{inf}}}{2}\right)^2\right)\\[1.4em] &\qquad+\pi\times\left(\frac{d_{\mathrm{sup}}}{2}\right)^2\times h_{\mathrm{cylindre}} \end{split}

où :

  • dsupd_{\mathrm{sup}} – diamètre supérieur du tronc de cône
  • dinfd_{\mathrm{inf}} – diamètre inférieur du tronc de cône
  • hco^neh_{\mathrm{cône}} et hcylindreh_{\mathrm{cylindre}} – les hauteurs des deux cuves

Pour calculer le réservoir partiellement rempli, il suffit d'additionner la partie tronc de cône et la partie cylindre, en fonction du niveau du liquide rempli, en utilisant les équations ci-dessus.

Le calcul du volume total du réservoir à fond conique est exactement le même que celui du réservoir à fond conique. La seule différence réside dans la détermination de la partie remplie - bien sûr, la partie cylindrique est d'abord remplie, et ensuite seulement le tronc de cône.

🙋 Vous avez calculé tous vos volumes en utilisant des unités métriques, mais vous avez besoin d'unités impériales ? Ne vous inquiétez pas, Omni dispose d'une solution pratique pour répondre à tous vos soucis : utilisez notre outil de conversion de volume pour convertir rapidement les unités de volume !

FAQ

Comment calculer le volume d'un réservoir d'eau ?

Vous pouvez essayer le calculateur de volume d'une cuve d'Omni Calculator ou procéder comme suit :

  1. Obtenez le rayon intérieur et la hauteur du réservoir.
  2. Élevez au carré le rayon, puis multipliez par pi (3,141 59...). Félicitations, vous avez obtenu l'aire du réservoir d'eau.
  3. Multipliez le résultat par la hauteur, et vous obtiendrez le volume du réservoir.

Comment calculer la cylindrée de mon moteur ?

Les experts automobiles l'appellent la cylindrée du moteur, et vous pouvez la calculer comme suit :

  1. Obtenez le volume de l'un des cylindres de votre moteur. Vous pouvez essayer le calculateur de volume d'une cuve de l'outil Omni Calculator ou obtenir le rayon et la hauteur du cylindre (course du piston du moteur).

  2. Élevez au carré le rayon, multipliez par pi (3,141 59...), puis par la course du piston.

  3. Multipliez le volume d'un cylindre par le nombre de cylindres de votre moteur, et vous obtiendrez la cylindrée du moteur.

Combien de temps l'eau stockée peut-elle durer dans une cuve ?

Cela dépend de la quantité d'eau stockée et du débit d'écoulement.

  1. Calculez le volume de votre cuve d'eau avec le calculateur de volume d'une cuve d'Omni Calculator. Obtenez la valeur en litres.
  2. Déterminez le nombre de litres que vous consommez par jour.
  3. Divisez la quantité d'eau dont vous disposez par votre consommation quotidienne. Le résultat est le nombre de jours d'eau dont vous disposez.

Pourquoi préférer les réservoirs d'eau cylindriques aux réservoirs carrés ?

Il y a deux raisons principales pour lesquelles nous préférons les réservoirs cylindriques aux réservoirs rectangulaires :

  1. Les réservoirs cylindriques résistent mieux aux contraintes que les réservoirs rectangulaires. Les fabricants ont donc besoin de moins de matériaux pour les construire.
  2. Les réservoirs rectangulaires sont plus difficiles à nettoyer, en particulier dans les coins.

Quel est le volume d'un baril de pétrole ?

218,7 L. Un baril de pétrole a un diamètre de 0,572 m et une hauteur de 0,851 m. Introduisez ces chiffres dans la formule suivante :

volume = π × (d/2)² × h = 3,141 × (0,572/2)² × 0,851 = 0,218 7 m² = 218,7 L

Image montrant une cuve cylindrique verticale dont les dimensions sont indiquées.

© Omni Calculator

Dimensions

Volume

Notre calculateur vous a-t-il aidé à résoudre votre problème ?

Check out 7 similar water tank and vessels calculators 🏊

Fire flow

Gallons per minute

Liters per minute