Winkelgeschwindigkeit Rechner

Dieser Winkelgeschwindigkeit-Rechner ist ein einfach zu bedienendes Werkzeug, das eine sofortige Antwort auf die Frage „Wie berechne ich die Winkelgeschwindigkeit?“ gibt. Im Text findest du mehrere Winkelgeschwindigkeitsformeln, lernst verschiedene Winkelgeschwindigkeitseinheiten kennen und kannst schließlich die Winkelgeschwindigkeit der Erde schätzen!

Hast du dich schon einmal gefragt, wie die Beziehung zwischen Winkelgeschwindigkeit und Winkelfrequenz ist? Oder wo die Winkelgeschwindigkeit angewendet wird? Lies weiter, um es herauszufinden, und werde ein Experte auf dem Gebiet der Kreisbewegung.

Die Winkelgeschwindigkeit beschreibt die Rotationsbewegung von Körpern. Sie misst, wie schnell sie sich um einen Drehpunkt bewegen. Wir können uns zwei verschiedene Arten von Drehungen vorstellen. Die erste beschreibt die Bewegung des Massenschwerpunkts eines bestimmten Objekts um einen bestimmten Punkt im Raum, den wir als Ursprung bezeichnen können. Einige Beispiele sind Planeten, die sich um die Sonne bewegen, oder ein Auto, das auf der Autobahn eine Ausfahrt nimmt.

Bei der zweiten Art von Drehung geht es um die Drehung des Körpers um seinen eigenen Massenschwerpunkt – den Spin (nicht zu verwechseln mit der Quanteneigenschaft von Teilchen, die auch Spin genannt wird). Sicherlich hast du schon einmal einen Basketballspieler gesehen, der einen Ball auf seinem Finger dreht.

Generell können wir sagen, je schneller die Bewegung, desto höher die Winkelgeschwindigkeit. In den Gleichungen für die Winkelgeschwindigkeit, die im nächsten Abschnitt beschrieben werden, müssen wir einige spezifische Werte festlegen.

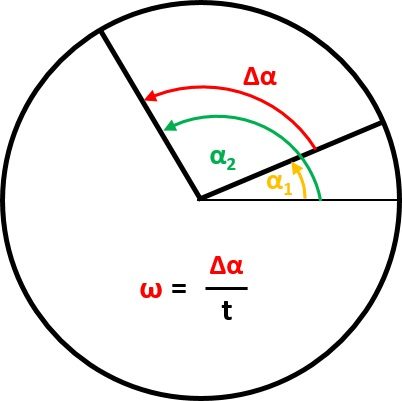
Dieser Winkelgeschwindigkeit-Rechner verwendet zwei verschiedene Formeln für die Winkelgeschwindigkeit, je nach deinen Eingabeparametern.

Die erste Gleichung ist analog zur Gleichung für die lineare Geschwindigkeit:

dabei sind $\alpha_1$ und $\alpha_2$ zwei Winkelwerte auf einem Kreis und $\Delta\alpha$ ist ihre Differenz. $t$ ist die Zeit, in der die Winkelveränderung stattfindet. Wie du siehst, gibt es für die normale Geschwindigkeit ein Verhältnis der Positionsverschiebung in einer Periode, während wir hier den Winkel statt der Entfernung verwenden.

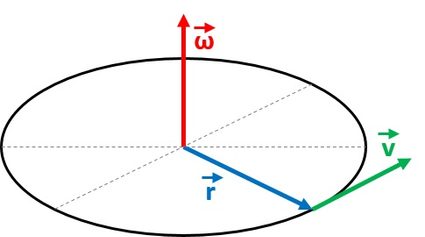
Wir können die zweite Formel für die Winkelgeschwindigkeit aus der Beziehung zwischen der linearen Geschwindigkeit und dem Radius ableiten, indem wir das Kreuzprodukt verwenden:

Wir können diesen Ausdruck umformulieren, um die Gleichung der Winkelgeschwindigkeit zu erhalten:

wobei alle diese Variablen Vektoren sind und $|r|$ den absoluten Wert des Radius angibt. Eigentlich ist die Winkelgeschwindigkeit ein Pseudovektor, dessen Richtung senkrecht zur Ebene der Rotationsbewegung steht.

Es gibt mehrere Einheiten für die Winkelgeschwindigkeit. Die Einheiten, die wir in unserem Rechner verwenden, sind unten aufgeführt:

• rad/s oder Radiant pro Sekunde — Die Definition stammt direkt aus der ersten Winkelgeschwindigkeitsformel. Sie gibt an, wie groß die Drehung (oder der Winkel) ist, die der Körper in einer bestimmten Zeit durchläuft.

• u/min oder Umdrehungen pro Minute — Die Einheit, die in der Praxis am häufigsten verwendet wird. Mit ihr kannst du beschreiben, wie schnell sich ein Rad oder ein Motor dreht. Du kannst dir den Unterschied zwischen 10 und 100 Umdrehungen pro Minute leicht vorstellen.

• hz oder Hertz — Die gleiche Einheit wird für die Frequenz verwendet, aber selten im Zusammenhang mit der Winkelgeschwindigkeit. Sie ähnelt u/min und gibt an, wie viele vollständige Umdrehungen in einer bestimmten Zeit gemacht werden. Der Unterschied besteht darin, dass die Grundeinheit der Zeit früher eine Minute war, während sie hier eine Sekunde ist.

Alle diese Einheiten der Winkelgeschwindigkeit werden mithilfe der folgenden Beziehungen ineinander umgerechnet:

1 RMP = 0,10472 rad/s = 0,01667 Hz;

oder andersherum:

1 Hz = 6,283 rad/s = 60 RPM.

Sieh dir die Definition der Winkelfrequenz an:

wobei $f$ die Frequenz ist. Wie wir sehen können, wird sie mit demselben Buchstaben bezeichnet. Außerdem ist die Einheit der Winkelfrequenz rad/s, also genau die gleiche wie bei der Winkelgeschwindigkeit. Es stellt sich also die Frage: „Was ist der Unterschied zwischen Winkelgeschwindigkeit und Winkelfrequenz?“.

Die Antwort ist relativ einfach. Die Beziehung zwischen der Winkelfrequenz und der Winkelgeschwindigkeit ist analog zu der zwischen der Geschwindigkeit und der Drehzahl. Erstere ist eine Größe der letzteren, d. h. die Winkelfrequenz ist ein Skalar, während die Winkelgeschwindigkeit ein (Pseudo-)Vektor ist.

Wir verwenden die Winkelfrequenz üblicherweise, wenn wir über eine harmonische Bewegung sprechen, wie zum Beispiel bei einem einfachen Pendel. Wie du dir vorstellen kannst, muss die Bewegung nicht durch eine Standarddrehung dargestellt werden, sondern nur durch eine Bewegung, die ihre Position periodisch wiederholt. Die Winkelgeschwindigkeit ist jedoch eng mit der Bewegung um einen bestimmten Punkt verbunden. Daher können wir sagen, dass die Winkelfrequenz eine allgemeinere Größe ist und wir sie zur Beschreibung einer Vielzahl physikalischer Probleme verwenden können. Im Gegensatz dazu umfasst die Winkelgeschwindigkeit nur die Rotationsbewegung.

Wie wäre es, wenn wir unseren Winkelgeschwindigkeit-Rechner benutzen? Schätzen wir die Winkelgeschwindigkeit der Erde! Als Erstes betrachten wir die Rotationsgeschwindigkeit. Wir wissen, dass die Erde in Bezug auf ferne Sterne eine volle Umdrehung in etwa 23 h 56 min 4 s macht, was ungefähr 23,934 h entspricht. Die gesamte Umdrehung entspricht dem Winkel 2π rad, somit ist die resultierende Winkelgeschwindigkeit:

oder $7,\!292 \cdot 10^{-5}\ \rm rad/s$ (in wissenschaftlicher Notation).

Da wir nun die Winkelgeschwindigkeit der Erde kennen, können wir ihre lineare Geschwindigkeit am Äquator bestimmen. Dazu brauchen wir den Radius der Erde, etwa 6371 km. Das Einzige, was wir tun müssen, ist, die Werte in die zweite Formel für die Winkelgeschwindigkeit einzusetzen:

Um die lineare Geschwindigkeit in Bezug auf den Erdmittelpunkt zu berechnen, musst du nur das Ergebnis mit dem Kosinus des Breitengrades deiner Stadt multiplizieren.

Hast du dich schon mal gefragt, warum Raketen normalerweise von Raumfahrtzentren in Äquatornähe und nicht von den Polen aus starten? Nun, ein Schub von fast 500 m/s zu Beginn ist ein beträchtlicher Bruchteil der Endgeschwindigkeit. Wenn du also den Startpunkt so nah wie möglich an den Äquator verlegst, brauchst du weniger Treibstoff, um die Rakete zu beschleunigen.

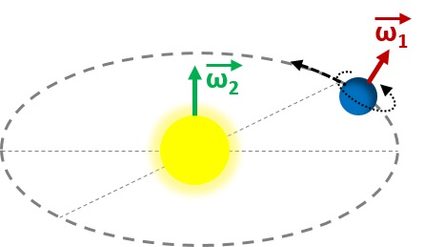
Danach können wir noch einmal fragen, wie man die Winkelgeschwindigkeit der Erde findet, aber diesmal die der Umlaufbahn. Alle Berechnungen sind analog, aber wir müssen die Zeit von 23,943 h in 1 Jahr ändern, was rund 365,25 Tage sind. Die Winkeländerung ist die gleiche, die komplette Umdrehung.

und die lineare Geschwindigkeit der Erde in Bezug auf die Sonne (für den Durchschnittsradius $\small 1,\!496\!\cdot\!10^8\ \rm km$) beträgt:

Wir bewegen uns ziemlich schnell, nicht wahr?

Es gibt viele physikalische Größen, die mit der Winkelgeschwindigkeit zusammenhängen, einige davon sind unten aufgeführt:

1. Winkelbeschleunigung — Beschreibt, wie sich die Winkelgeschwindigkeit mit der Zeit verändert. Je größer der Unterschied zwischen den Winkelgeschwindigkeiten ist, desto größer ist die Winkelbeschleunigung. Wie das in der Praxis funktioniert, kannst du mit unserem Winkelbeschleunigungsrechner 🇺🇸 überprüfen.

2. Rotationskinetische Energie — Das Maß für die Energie einer Kreisbewegung. Wie bei der kinetischen Energie ist die Abhängigkeit von der (Winkel-)Geschwindigkeit quadratisch.

3. Zentrifugalkraft — Sie macht sich in einem Fahrzeug beim Abbiegen bemerkbar. Umso schneller du eine Kurve fährst oder je schärfer sie ist, desto größer wird die Zentrifugalkraft, die wir deutlich spüren können.

4. Koriolis-Effekt — Dieser bewirkt, dass sich Objekte drehen, wenn sie sich auf einem rotierenden Körper (z. B. auf der Erde) befinden, anstatt sich in einer geraden Linie zu bewegen.

5. Riemenscheibensystem — Das ist genau genommen keine physikalische Größe, aber es ist ein interessantes Gerät, bei dem sich alles um die Winkelgeschwindigkeit dreht. Das einfachste System besteht aus zwei Riemenscheiben, die normalerweise unterschiedliche Umfänge oder Radien haben. Ein Riemen verbindet sie miteinander, sodass ihre linearen Geschwindigkeiten identisch sind, aber da sie unterschiedlich groß sind, ändern sich ihre Winkelgeschwindigkeiten proportional.

   Wenn wir das wissen und einen Motor mit einer genau definierten Drehgeschwindigkeit haben, können wir die Winkelgeschwindigkeit des Abtriebselements mit guter Genauigkeit einstellen, indem wir einfach seine Größe anpassen.

Es gibt einige grundlegende Regeln, die uns sagen, welche Größen in isolierten Systemen erhalten bleiben. Die bekanntesten sind die Erhaltung der Energie und die Erhaltung des Schwungs. Zusammen mit ihnen gibt es auch die Erhaltung des Drehimpulses. Wenn wir an zwei Momente in der Zeit denken, können wir die Regel wie folgt formulieren:

wobei $I_1$ und $I_2$ die anfänglichen bzw. endgültigen Massenträgheitsmomente sind; diese Größen beschreiben die Verteilung der Masse auf ihre jeweiligen Drehpunkte.

Wir können sehen, dass, wenn das Trägheitsmoment zunimmt, die Winkelgeschwindigkeit abnimmt und umgekehrt. Was sind nun die Folgen dieses Phänomens?

Stellen wir uns vor, du bist Eiskunstläufer. Wenn du dich drehst, besitzt du eine gewisse Winkelgeschwindigkeit. Wenn deine Arme weit geöffnet sind, ist das Massenträgheitsmoment relativ groß. Dann nimmst du deine Arme dicht an deinen Körper heran. Infolgedessen sinkt dein Trägheitsmoment, und da der Gesamtdrehimpuls erhalten bleiben muss, steigt deine Winkelgeschwindigkeit — das heißt, du drehst dich schneller! Das ist keine Magie, sondern Physik!

Wenn du nicht Eiskunstlaufen kannst/magst, versuche, dies mit einem normalen Drehstuhl zu überprüfen. Aber denk daran: Sicherheit geht vor! Vergewissere dich, dass genügend Platz für dieses Experiment vorhanden ist. Danach fängst du einfach an, dich zu drehen und beobachtest, wie sich deine Winkelgeschwindigkeit verändert, wenn du deine Arme ausbreitest und an dich zurücknimmst. Du kannst den Effekt zusätzlich verstärken, indem du ein paar Hanteln benutzt. So kannst du Bewegung und Spaß vereinen!