Omni Calculator logo
Zuletzt aktualisiert:

Widerstandsmoment Rechner

Neu

Inhalt

Wie berechnet man das Widerstandsmoment aus dem Trägheitsmoment?Plastisches Widerstandsmoment: über das elastische Widerstandsmoment hinausWiderstandsmoment Formeln für rechteckige Querschnitte und andere FormenWas sind die Einheiten des Flächenträgheitsmoments?FAQs

Dieses Tool berechnet das Widerstandsmoment, eine der wichtigsten geometrischen Eigenschaften bei der Bemessung von Trägern, die einer Biegung ausgesetzt sind. Außerdem berechnet es das Trägheitsmoment der neutralen Achse und das Flächenträgheitsmoment der gängigsten Profile (wenn du nur das Trägheitsmoment benötigst, schau dir unseren Trägheitsmoment Rechner an).

Die Formeln für das Widerstandsmoment eines Rechtecks oder Kreises sind relativ einfach zu berechnen. Bei komplexen Geometrien wie einem T-Stück, einer Rinne oder einem I-Träger kann ein Rechner jedoch Zeit sparen und helfen Fehler zu vermeiden.

In den folgenden Abschnitten erläutern wir die beiden Arten des Widerstandsmoments, wie man das Widerstandsmoment aus dem Trägheitsmoment berechnet, und stellen die Widerstandsmoment Formeln für ein Rechteck und viele andere gängige Formen vor.

Wie berechnet man das Widerstandsmoment aus dem Trägheitsmoment?

Das Widerstandsmoment wird von Ingenieuren verwendet, um die maximale mechanische Spannung, die ein Biegemoment auf einen Balken ausübt, schnell vorherzusagen. Die Gleichung für den maximalen Absolutwert der mechanischen Spannung in einem auf Biegung beanspruchten Balken lautet:

σm=McI\sigma_m = \frac{Mc}{I}

wobei:

  • σm\sigma_m — Maximaler absoluter Wert der mechanischen Spannung in einem bestimmten Trägerabschnitt;
  • MM — Biegemoment, dem der Träger in diesem Abschnitt ausgesetzt ist;
  • cc — Größter Abstand zwischen der neutralen Achse und der Oberfläche des Trägers; und
  • II — Flächenträgheitsmoment (auch bekannt als Flächenmoment 2) um die neutrale Achse des Querschnitts (ebenfalls mit diesem Tool berechnet).

Bei einem Kreis beispielsweise entspricht der größte Abstand dem Radius, während er bei einem Rechteck der halben Höhe entspricht.

Da das Verhältnis I/cI/c nur von den geometrischen Merkmalen abhängt, können wir daraus eine neue geometrische Eigenschaft definieren, das sogenannte Widerstandsmoment, das mit dem Buchstaben SS bezeichnet wird:

S=IcS = \frac{I}{c}

Wie auch das Flächenträgheitsmoment ist diese neue geometrische Eigenschaft in vielen Tabellen und Rechnern zu finden. Wenn du aber wissen möchtest, wie du das Widerstandsmoment aus dem Trägheitsmoment berechnen kannst, musst du nur II durch cc dividieren, um es zu erhalten.

Schließlich können wir das Widerstandsmoment mit der mechanischen Spannung und dem Moment in Beziehung setzen:

σm=MS\sigma_m = \frac{M}{S}

🙋 Kommt dir diese Beziehung bekannt vor? Diese Beziehung entspricht der Gleichung für die mechanische Spannung: σ=FA\sigma = \frac{F}{A}. Das Biegemoment entspricht der axialen Kraft, während das Widerstandsmoment der Querschnittsfläche entspricht. Du kannst unseren Mechanische Spannung Rechner benutzen, um die mechanische Spannung zu ermitteln.

Berücksichtige diese Überlegungen bei der Berechnung des Widerstandsmoments und der maximalen Spannungen:

  • Das Biegemoment erhalten wir durch eine statische oder strukturelle Analyse des Trägers.
  • Um das Widerstandsmoment zu ermitteln, können wir Tabellen für vordefinierte Bauteile verwenden, aber dieser Rechner ist die beste Option, wenn du es mit benutzerdefinierten Geometrien zu tun hast.
  • Wenn wir (wie üblich) einen Balken mit gleichmäßigem Querschnitt betrachten, befindet sich der Ort der maximalen mechanischen Spannung an der Stelle des maximalen Biegemoments. Wenn das nicht der Fall ist, kann σm\sigma_m an einer anderen Stelle liegen.
  • Die obigen Formeln gelten für Materialien, die sich elastisch verhalten und dem Hookeschen Gesetz gehorchen. Wenn es sich nicht elastisch, sondern plastisch verformt, müssen wir das plastische Widerstandsmoment verwenden.

Plastisches Widerstandsmoment: über das elastische Widerstandsmoment hinaus

Die vorstehenden Gleichungen gelten nicht, wenn ein Balkenmaterial Spannungen über die Streckgrenze hinaus ausgesetzt wird, da sie davon ausgehen, dass Spannung und Dehnung linear miteinander verbunden sind. In diesem Fall müssen wir das plastische Widerstandsmoment verwenden. Ähnlich wie das elastische Widerstandsmoment SS stellt auch das plastische Widerstandsmoment eine Beziehung zwischen mechanischer Spannung und Moment her:

Mp=ZσYM_p = Z\sigma_Y

wobei:

  • MpM_p — Plastisches Moment des Querschnitts;
  • ZZ — Plastisches Widerstandsmoment; und
  • σY\sigma_Y — Streckgrenze des Bauteilmaterials.

Das plastische Moment bezieht sich auf das Moment, das erforderlich ist, um eine plastische Verformung über die gesamte Querschnittsfläche eines Bauteils zu bewirken.

Der Nutzen der letzten Gleichung besteht darin, dass wir das Biegemoment, das zu einer plastischen Verformung führt, vorhersagen können, wenn wir nur die Dehngrenze und das plastische Widerstandsmoment kennen.

Die folgende Grafik beschreibt besser, worauf wir uns beziehen, wenn wir über plastische Momente sprechen:

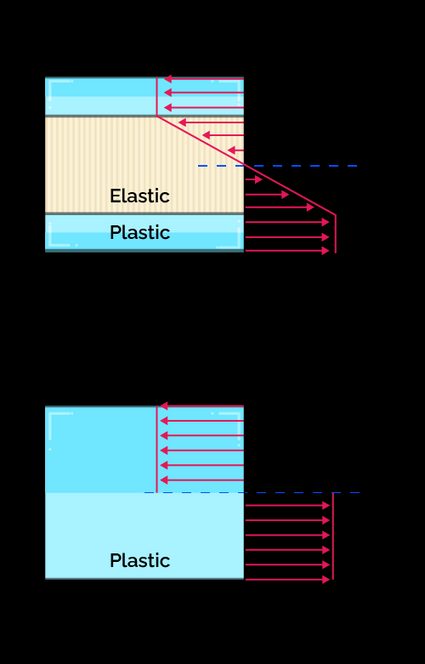
Bild der Spannungsverteilung bei plastischer Verformung
Grafische Darstellung der Verteilung der mechanischen Spannung bei plastischen Verformungen. Wir gehen von einem perfekten Plastizitätsmodell aus; daher sind die mechanischen Spannungen in Wirklichkeit nicht so gleichmäßig verteilt.

Damit es zu einer plastischen Verformung kommt, müssen wir eine mechanische Spannung erzeugen, die der Streckgrenze des Materials entspricht. Wie du siehst, ist der Übergang von elastisch zu plastisch nicht gleichmäßig über das gesamte Bauteil verteilt, da einige Bereiche die Streckgrenze vor anderen erreichen.

Sobald der gesamte Querschnitt die Streckgrenze erreicht, kommt es zu einer plastischen Verformung des gesamten Querschnitts. Das dafür erforderliche Biegemoment wird als plastisches Moment bezeichnet.

Widerstandsmoment Formeln für rechteckige Querschnitte und andere Formen

In der folgenden Tabelle findest du die Formel für das Widerstandsmoment für rechteckige Querschnitte und viele andere Profile (Scroll die Tabelle seitwärts, um alle Gleichungen zu sehen):

Form

Elastisches Widerstandsmoment

Quadratisch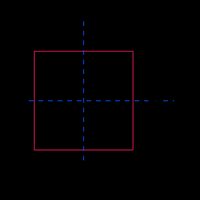

Bild eines quadratischen Querschnitts und seiner Abmessungen

yc=xc=a/2y_c = x_c = a/2

Ix=Iy=a412I_x = I_y = \frac{a^4}{12}

Sx=Sy=Ixyc=a36S_x = S_y =\frac{I_x}{y_c} = \frac{a^3}{6}

Rechteck

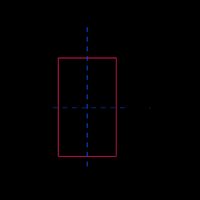Bild eines rechteckigen Querschnitts und dessen Abmessungen

yc=d/2y_c=d/2

xc=b/2x_c=b/2

Ix=bd312I_x = \frac{bd^3}{12}

Iy=db312I_y = \frac{db^3}{12}

Sx=Ixyc=bd26S_x = \frac{I_x}{y_c} = \frac{b d^2}{6}

Sy=Iyxc=db26S_y = \frac{I_y}{x_c} = \frac{d b^2}{6}

Hohles Rechteck (Rechteckrohr)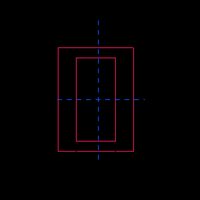

Bild eines hohlen Rechteckquerschnitts und seiner Abmessungen

yc=d/2y_c=d/2

xc=b/2x_c=b/2

Ix=bd3−bidi312I_x = \frac{bd^3-b_id_i^3}{12}

Iy=db3−dibi312I_y = \frac{db^3-d_ib_i^3}{12}

Sx=IxycS_x = \frac{I_x}{y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

T-Stück

Bild eines hohlen T-Stücks und seiner Abmessungen

yc=bt2+twd(2t+d)2(tb+twd)y_c=\frac{bt^2+t_wd(2t+d)}{2(tb+t_wd)}

xc=b/2x_c=b/2

A=tb+twdA = tb + t_wd

Ix=b(d+t)3−d3(b−tw)3          −A(d+t−yc)2I_x = \frac{b(d+t)^3-d^3(b-t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ - \footnotesize A(d+t-y_c)^2

Iy=tb3+dtw312I_y = \frac{tb^3+dt_w^3}{12}

Sx=Ixd+t−ycS_x = \frac{I_x}{d+t-y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

Hohlabschnitt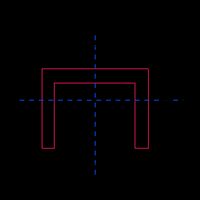

Bild eines hohlen Rechteckabschnitts und seiner Abmessungen

yc=bt2+2twd(2t+d)2(tb+2twd)y_c=\frac{bt^2+2t_wd(2t+d)}{2(tb+2t_wd)}

xc=b/2x_c=b/2

Ix=b(d+t)3−d3(b−2tw)3          −A(d+t−yc)2I_x = \frac{b(d+t)^3-d^3(b-2t_w)}{3} \\\ \ \ \ \ \ \ \ \ \ -\footnotesize A(d+t-y_c)^2

Iy=(d+t)b3−d(b−2tw)312I_y = \frac{(d+t)b^3-d(b-2t_w)^3}{12}

Sx=Ixd+t−ycS_x = \frac{I_x}{d+t-y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

A=tb+2twdA = tb + 2t_wd

Breitflanschträger (gleiche Flansche)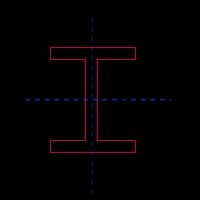

Bild eines hohlen Rechteckprofils und seiner Abmessungen

yc=d/2+ty_c=d/2+t

xc=b/2x_c=b/2

Ix=b(d+2t)3−(b−tw)d312I_x = \frac{b(d+2t)^3-(b-t_w)d^3}{12}

Iy=b3t6+tw3d12I_y = \frac{b^3t}{6} + \frac{t_w^3d}{12}

Sx=IxycS_x = \frac{I_x}{y_c}

Sy=IyxcS_y = \frac{I_y}{x_c}

Winkel

Bild eines hohlen Rechteckausschnitts und seine Abmessungen

yc=d2+bt+−t22(b+d−t)y_c=\frac{d^2+bt+-t^2}{2(b+d-t)}

xc=b2+dt−t22(b+d−t)x_c=\frac{b^2+dt-t^2}{2(b+d-t)}

A=t(b+d−t)A = t(b+d-t)

Ix=bd3−(b−t)(d−t)33          −A(d−yc)2\footnotesize I_x = \frac{bd^3-(b-t)(d-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(d-y_c)^2

Iy=db3−(d−t)(b−t)33          −A(b−xc)2\footnotesize I_y = \frac{db^3-(d-t)(b-t)^3}{3} \\\ \ \ \ \ \ \ \ \ \ -A(b-x_c)^2

Sx=Ixd−ycS_x = \frac{I_x}{d-y_c}

Sy=Iyb−xcS_y = \frac{I_y}{b-x_c}

A=t(b+d−t)A = t(b+d-t)

Kreis

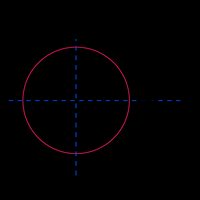Bild eines Kreisausschnitts und seiner Abmessungen

yc=xc=Ry_c = x_c = R

Ix=Iy=π4R4I_x = I_y = \frac{\pi}{4}R^4

Sx=Sy=Ixyc=π4R3S_x = S_y =\frac{I_x}{y_c} = \frac{\pi}{4}R^3

Hohlkreis oder Rohr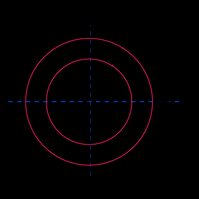

Bild eines kreisförmigen Hohlprofils und dessen Abmessungen

yc=xc=Ry_c = x_c = R

Ix=Iy=π4(R4−Ri4)I_x = I_y = \frac{\pi}{4}(R^4-R_i^4)

Sx=Sy=IxycS_x = S_y =\frac{I_x}{y_c}

🔎 Möchtest du Durchbiegungen statt mechanischer Spannungen berechnen? Wir haben einen Träger Durchbiegung Rechner.

Was sind die Einheiten des Flächenträgheitsmoments?

Die Einheiten des Flächenträgheitsmoments sind mm⁴ oder m⁴ im Internationalen Einheitensystem und in⁴ im US-amerikanischen Einheitensystem. Die Einheiten des elastischen Widerstandsmoments sind mm³, m³ und in³.

FAQs

Wie berechnet man das Widerstandsmoment eines Rohrpfahls?

Um das Widerstandsmoment eines Rohrpfahls mit der Dicke t und dem Radius R zu berechnen, verwende die Widerstandsmoment-Formel für einen sehr dünnen Ring: S = πR²t, oder befolge diese Schritte:

  1. Miss den Radius R und die Dicke t des Rohrpfahls.
  2. Multipliziere die Zahl π mit dem Quadrat des Radius.
  3. Multipliziere das letzte Ergebnis mit der Dicke.
  4. Das war's! Du kannst auch unseren Widerstandsmoment-Rechner benutzen und es schneller machen.

Wenn das Rohr dicker ist, kannst du es mit unserem Widerstandsmoment-Rechner berechnen.

Was sind die Einheiten des Widerstandsmoments?

Die Einheiten des elastischen Widerstandsmoments sind mm³ oder m³ im Internationalen Einheitensystem und in³ in den Vereinigten Staaten. Seltsamerweise sind das die gleichen Einheiten wie für das Volumen.

Was sind gängige Standardmaße von Holzbalken?

Du kannst für Holzbalken verschiedene Standardmaße finden, die sich nach Breite, Höhe und Länge unterscheiden. In Deutschland sind gängige Abmessungen in Millimetern angegeben, z. B. 44 × 100, 75 × 125 oder 100 × 200. Für exakte Maße kannst du in den DIN-Normen DIN 4074-1 und DIN EN 336 nachschauen, wobei die Werte auch hier leicht abweichen dürfen. In der Regel werden Bauhölzer als Balken bezeichnet, wenn mindestens eine Seite im Querschnitt breiter als zwanzig Zentimeter ist.

Wie lautet die Formel für das Widerstandsmoment für einen rechteckigen Querschnitt?

Die Formel für das elastische Widerstandsmoment eines Rechtecks lautet S = bd²/6, wobei:

  • S — Widerstandsmoment;
  • b — Höhe des Rechtecks; und
  • d — Basis oder Breite des Rechtecks.

Beachte, dass sich dieses Widerstandsmoment um die horizontale Mittelachse dreht.

Wir können die Widerstandsmoment-Formel für einen rechteckigen Querschnitt ableiten, indem wir sein Flächenträgheitsmoment (bh³/12) durch den maximalen Abstand von der neutralen Achse (h/2) dividieren:

S = (bh³/12)/(h/2) = bh²/6.

Wie lautet die Widerstandsmoment-Formel für einen quadratischen Querschnitt?

Die Formel für das elastische Widerstandsmoment eines Quadrats lautet S = a³/6, wobei:

  • S — Widerstandsmoment; und
  • a — Die Länge einer der Seiten des Quadrats;

Wir können die Widerstandsmomentformel für einen quadratischen Querschnitt ableiten, indem wir sein Flächenträgheitsmoment (a⁴/12) durch den maximalen Abstand von der neutralen Achse (a/2) teilen:

S = (a⁴/12)/(a/2) = a³/6.

Wie berechne ich das plastische Widerstandsmoment eines I-Profils?

Um das plastische Widerstandsmoment eines I-Profils zu berechnen, wende die Formeln an:

  • Zₓ = 0,25d²tᵥᵥ + bt(d + t);
  • Zᵧ = 0,5b²t + 0,25dtᵥᵥ²;

wobei:

  • Zₓ — Plastisches Widerstandsmoment um die horizontale plastische Neutralachse;
  • Zᵧ — Plastisches Widerstandsmoment um die vertikale plastische neutrale Achse;
  • d — Steglänge;
  • tᵥᵥ — Stegdicke;
  • t — Flanschdicke; und
  • b — Flanschlänge.

Eingaben

Bild eines rechteckigen Ausschnitts.

© Omni Calculator

Im Abschnitt „Formeln für Widerstandsmomente” des Artikels stellen wir die Formeln vor, mit denen Widerstandsmomente berechnet werden. Wenn du denkst, dass wir eine wichtige Form übersehen haben, lass es uns wissen.

Check out 38 similar materials and continuum mechanics calculators 🧱
Angle of reposeAngle of twistBend allowance...35 more