Flache Erde vs Runde Erde Rechner

Was ist wohl der beste Weg, um die Welt zu erforschen? Eine Theorie aufstellen und versuchen, diese durch Beobachtungen zu beweisen (Wissenschaft)? Oder etwas ohne viel Nachzudenken zu erfinden und offensichtliche Fakten ignorieren (Unsinn)? Hier bei Omni sind wir der Meinung, dass die erste Option am besten funktioniert. Diese Einstellung hat uns auf den Mond gebracht, nicht wahr? – Das hat sie übrigens wirklich!

Zum Welttag der Wissenschaft für Frieden und Entwicklung, der jedes Jahr am 10. November stattfindet, haben wir einen Rechner entwickelt, der dir hilft, gegen Quatsch, Halbwahrheiten und Blödsinn und für Wissenschaft, Beobachtung und Aufgeschlossenheit zu kämpfen.

Omnis Flache Erde vs. Runde Erde-Rechner enthält eine Reihe von Experimente, die beweisen, dass die Erde tatsächlich eine Kugel ist. Keine Sorge, du wirst keine eigene Rakete bauen müssen, die ins Weltall fliegt, um dies zu überprüfen (oder den Impuls und die Impulserhaltung und die kinetische Energie der Erde berechnen zu müssen).

Wir haben drei simple Experimente zum Nachmachen für dich zusammengefasst:

• Der doppelte Sonnenuntergang – Indem du deinen Blickwinkel über dem Boden änderst, kannst du einen Sonnenuntergang zweimal sehen. Unser Rechner sagt dir, wie viel du vom zweiten Sonnenuntergang sehen wirst.

• Verschwindende Objekte – Lass Objekte hinter der Erdkrümmung verschwinden, indem du die Höhe deines Blickwinkels änderst. Dieser Rechner sagt dir, wie hoch ein Objekt ist, das du verschwinden lassen kannst.

• Der Stockschatten – Nutze die Länge des Schattens, den ein Stock an verschiedenen Stellen wirft, um den Umfang der Erde zu schätzen.

Bevor wir zu den Experimenten kommen, möchten wir uns kurz ansehen, wieso Menschen an eine flache Erde glauben und welche Weltanschauung sie vertreten.

Erstaunlicherweise ist sich im reichsten und technologisch am weitesten entwickelten Land der Welt jeder sechste Einwohner unsicher, ob die Erde rund ist 🤔. Es handelt sich dabei um die USA. Der Glaube an eine flache Erde könnte auf die stark individualistische Kultur und das Misstrauen gegenüber Autoritäten, Institutionen und Experten zurückzuführen sein.

Flat-Earther scheinen die Welt ganz anders zu betrachten, ohne Bezug auf jegliche menschliche Entdeckungen der letzten 2000 Jahre. Wow, die haben was verpasst. Außerdem sind sie extrem misstrauisch gegenüber allen Fakten, die sie nicht selbst überprüft haben.

Sie nehmen die außergewöhnlichsten Herausforderungen an, um zu beweisen, dass die Erde flach ist, obwohl mit einfachen Experimenten bewiesen werden kann, dass die Erde rund ist. Hier sind einige Beispiele:

• "Mad" Mike Hughes baute seine eigenen dampfbetriebenen Raketen, um auf eine Höhe von 550 m zu fliegen und die fehlende Krümmung der Mojave-Wüste zu fotografieren. Leider muss man mindestens 11 000 m hochfliegen, um die Krümmung der Erde sehen zu können. Er kam im Februar 2020 tragisch bei einem missglückten Raketenflug ums Leben.
• Der YouTube-Star Logan Paul plante in die Antarktis reisen, um den Rand der flachen Erde zu finden. Die Reise fand jedoch aufgrund der COVID-19-Pandemie und des Mangels an medizinischen Einrichtungen für eventuelle Notfälle nicht statt.
• Der Rapper B.o.B versuchte, per Crowdfunding seinen eigenen Satellitenstart zu finanzieren, um zu beweisen, dass die Erde eine Scheibe ist. Von geplanten 1 Million $ für dieses Projekt, schaffte er es aber nur, 6883 $ zu sammeln. Na ja, was soll's. Vielleicht kann er stattdessen unsere einfachen, kostengünstigen Experimente ausprobieren.

Dieser Cartoon von Tom Fonder fasst die Flat Earthers ziemlich gut zusammen.

Im Modell der flachen Erde ist die Welt eine Scheibe (ähnlich den Zahnrädern, die für die Getriebeübersetzungen verwendet werden), in welcher sich der Nordpol in der Mitte befindet. Um den Rand der Scheibe herum befindet sich das Eis und der Schnee des „Südpols”. Dieser bildet dann eine eisige Barriere, die vermutlich verhindern soll, dass das Wasser der Ozeane von der Scheibe ins All fällt.

Die Dicke der flachen Erdscheibe ist nicht klar. Die Masse muss jedoch viel geringer sein als die einer runden Erde, damit die Erdatmosphäre aufrechterhalten werden kann. Vielleicht gibt es eine transparente Kuppel über der Erde, die verhindert, dass die Atmosphäre entweicht.

Beim Modell der flachen Erde befindet sich die Sonne über der Scheibe und kreist in einem geringen Abstand am Himmel. Das erklärt aber noch nicht die Sonnenaufgänge und Sonnenuntergänge. Stellen wir uns vor, dass sich die Erdscheibe wie eine Münze relativ zur Sonne dreht. Das würde zumindest unseren Sonnenaufgang und -untergang erklären. Allerdings gäbe es keine Zeitzonen, da Sonnenaufgang und -untergang überall auf der Welt zur gleichen Zeit stattfinden würden.

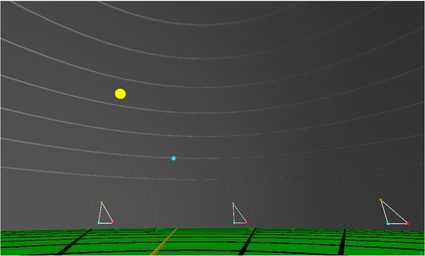
Das ist das Hauptproblem des Modells der flachen Erde. Es ist voller Widersprüchen und unerklärlicher Beobachtungen. Warum ist die Temperatur zum Beispiel sowohl in der Mitte als auch am Rand der Scheibe niedrig?

Kehren wir zu einer wissenschaftlicheren Denkweise zurück und lass uns das erste Experiment vorstellen.

Dieses erste Experiment ist ganz einfach durchzuführen. Bewege dich schnell genug nach oben, um dem Schattenwurf des Horizonts zuvorzukommen. So kannst du einen Teil des Sonnenuntergangs zweimal sehen! Wenn du dieses Phänomen beobachten kannst, dann ist die Erde tatsächlich rund. Mit unserem Rechner kannst du ermitteln, wie viel vom zweiten Sonnenuntergang du sehen kannst und wie lange ein Sonnenuntergang dauern kann.

Was würdest du sehen, wenn die Erde flach wäre? Keinen zweiten Sonnenuntergang 😭. Egal, wie schnell hoch du von der Oberfläche einer flachen Erde gehst, du würdest die Sonne erst wieder bei Sonnenaufgang sehen.

Für den Sonnenuntergang auf einer runden Erde, kannst du dir vorstellen, dass der Schatten, den der Erdhorizont wirft, auf dich zukommt und deinen Körper hinauf wandert. Wenn du diesem Schatten zuvorkommen kannst, indem du dich schnell genug nach oben bewegst, kannst du den Sonnenuntergang noch einmal sehen. Werfen wir einen Blick auf die Mathematik dahinter.

Dieser Artikel gibt uns eine Gleichung, die die Zeit mit der Höhe des Schattens in Beziehung setzt:

t = 8 ∙ √h,

wobei:

• t — die Zeit ist, die der Schatten braucht, um sich um den Betrag h in die Höhe zu bewegen und
• h — der Höhenunterschied zwischen zwei Höhen ist.

Da wir uns nicht in 0 Sekunden von der niedrigen zur hohen Höhe beamen können, müssen wir die Reisezeit berücksichtigen. Um herauszufinden, wie viel wir vom zweiten Sonnenuntergang sehen können, müssen wir die Dauer des Sonnenuntergangs kennen. Dann erhalten wir die folgende Gleichung für den Prozentsatz des zweiten Sonnenuntergangs, den du sehen wirst:

Sonnenuntergang in Prozent = 100 ∙ (1 - ((Sonnenuntergangsdauer - t - Reisezeit) / Sonnenuntergangsdauer))

Es gibt ein paar Möglichkeiten, die Sonne kurz nach ihrem Untergang noch einmal zu sehen, und zwar in unterschiedlichem Maße. Omni's Flache Erde vs. runde Erde-Rechner berechnet dir, wie viel von einem zweiten Sonnenuntergang du sehen kannst. Lass uns drei verschiedene Optionen durchgehen:.

1. Leg dich hin und steh auf

Was die Ausrüstung betrifft, ist diese Idee die einfachste. Du brauchst nur einen Ort, an dem du die Sonne im Meer oder auf sehr flachem Land (z. B. einer Wüste) untergehen sehen kannst. Ein schöner, wolkenloser Himmel ist ebenfalls hilfreich. Alles, was du tun musst, ist, den Sonnenuntergang zu beobachten, während du dich hinlegst. Sobald du nichts mehr von der Sonne sehen kannst, stehst du so schnell wie möglich auf. Du solltest wieder einen kleinen Teil des oberen Teils der Sonne sehen können.

Hier erfährst du, wie du mit dem Rechner genau ausrechnen kannst, wie viel der Sonne du beim zweiten Mal sehen wirst.

1. Wähle einen Ort aus, der dir am nächsten ist, oder gib die Dauer des Sonnenuntergangs an deinem Standort manuell ein.
2. Gib deine Augenhöhe beim Liegen ein. Wir empfehlen etwa 20 cm.
3. Gib ein, wie lange du brauchst, um die höhere Höhe zu erreichen. Wir schätzen, dass es etwa eine halbe Sekunde dauert. Miss die Zeit aber besser nach, um das zu überprüfen.
4. Gib deine Augenhöhe ein, wenn du aufrecht stehst. Du kannst sie messen, indem du den Abstand zwischen deinem höchsten Punkt deines Kopfes und deinen Augen von deiner Gesamtgröße abziehst.
5. Du erhältst dann den Prozentsatz der Sonne, den du noch sehen kannst. Der Prozentsatz ist dir zu gering? Versuche, die Werte im Rechner zu ändern oder schaue dir die fortgeschritteneren Varianten des Experiments unten an.

Mit dieser Methode solltest du etwa 5% des zweiten Sonnenuntergangs sehen können.

2. Schnelles Hochfahren im Fahrstuhl eines Wolkenkratzers

Um mehr vom zweiten Sonnenuntergang zu sehen, musst du den Höhenunterschied vergrößern und schneller erreichen, um dem Schatten des Horizonts voraus zu sein. Ein Wolkenkratzer mit einem schnellen Aufzug ist eine Möglichkeit. Dieses Phänomen wurde im Burj Khalifa Hotel in Dubai beobachtet.

Wähle für dieses Experiment aus der Ideenliste des Rechners „Wolkenkratzer-Fahrstuhl – Burj Khalifa Hotel” aus. Wenn du dies an einem anderen Gebäude ausprobieren möchtest, passe die Eingabewerte entsprechend an.

Du solltest in der Lage sein, 88% des Sonnenuntergangs noch einmal sehen zu können und die Dauer damit fast zu verdoppeln. Wenn du ein Sonnenuntergangliebhaber bist, ist das genau das Richtige für dich.

3. Drohne mit Kamera

Eine weitere Idee ist, eine hochwertige Drohne mit einer Live-Streaming-Kamera zu verwenden. Wir haben Drohnen gefunden, die 1000 m in 200 Sekunden erreichen können. Wenn du die Option „Drohne” aus der Ideenliste auswählst, wirst du sehen, dass du mit dieser Methode etwa ein Drittel des Sonnenuntergangs noch einmal sehen kannst.

Prüfe, wie schnell und hoch deine Drohne fliegen kann und passe die Werte im Rechner entsprechend an.

Mit diesem Experiment können wir einen Teil eines Objekts hinter der Erdkrümmung verschwinden lassen. Finde ein Gewässer, dessen Ufer mindestens 2 km entfernt ist, und führe das Experiment an einem ruhigen Tag ohne Wind durch.

Um den Fata Morgana-Effekt (Lichtbrechung) zu vermeiden, solltest du das Experiment am Morgen durchführen, wenn es kühl ist. Das ist auch der Grund, wieso es nicht empfehlenswert ist, das Experiment in einer Wüste durchzuführen – durch die Luftspiegelung kannst du die Objekte am anderen Ufer nicht deutlich genug sehen.

In diesem YouTube-Video lässt jemand einen 7 km entfernten Lkw auf der anderen Seite eines Sees verschwinden, indem er seine Kamera näher an den Boden heranführt.

Alternativ dazu ist auch ein Offshore-Windpark eine gute Demonstartion, wie dieses Foto zeigt:

Je weiter eine Windmühle entfernt ist, desto mehr wird von ihr verdeckt. Darum geht es in diesem Experiment – zu berechnen, wie viel von einem weit entfernten Objekt hinter der Erdkrümmung versteckt wird.

In diesem Experiment beginnen wir an einem hohen Aussichtspunkt und gehen dann zu einem niedrigen Aussichtspunkt hinunter, um ein entferntes Objekt zu verdecken. Mathematisch ausgedrückt: Wir finden heraus, wie viel aus der hohen und der niedrigen Ansicht verdeckt werden und berechnen die Differenz.

Um die verdeckte Höhe zu berechnen, müssen wir zunächst die Entfernung zum Horizont mit der folgenden Gleichung bestimmen:

a = √[(r + h)² - r²],

wobei:

• a die Entfernung zum Horizont ist,
• h die Sichthöhe über dem Boden ist und
• r der Radius der Erde ist, der 6371 km entspricht.

Das Ergebnis setzten in eine zweite Gleichung ein, die berechnet, wie viel von dem Objekt verdeckt wird, x, wenn es aus einer Höhe von null betrachtet wird:

x = √(a² - 2ad + d² + r²) - r.

Die Differenz zwischen den beiden Werten von x ist die Höhe des Objekts, die wir verschwinden lassen können, indem wir unsere Blickhöhe ändern.

OK, du hast also einen ausgezeichneten Ort gefunden, zum Beispiel einen See, dessen Ufer ein paar Kilometer entfernt ist. Um die Objekte am anderen Ufer zu sehen, brauchst du ein gutes Fernglas. Noch besser ist eine Videokamera mit einem starken Zoomobjektiv. Damit kannst du das Experiment auch aufzeichnen, so wie in dem Video oben.

Um einen ruhigen Blick durch dein Fernglas oder deine Kamera zu bekommen, solltest du sie auf einem Stativ befestigen. Mit diesem kannst du auch die beiden Höhen genau messen.

Hier erfährst du, wie du mit dem Rechner herausfinden kannst, wie groß das Objekt ist, das du hinter der Erdkrümmung verschwinden lassen möchtest.

1. Miss die Entfernung zum anderen Ufer des Sees. Du kannst dafür eine Karte oder die Messfunktion von Google Maps verwenden. Gib die Entfernung in die Variable „Entfernung zum Objekt” des Rechners ein.
2. Miss deine Augenhöhe über dem Boden, wenn du stehst, oder die hohe Position deiner Kamera. Gib diesen Wert in das nächste Eingabefeld ein.
3. Wiederhole den Schritt, wenn du liegst oder deine Kamera sich in der niedrigen Position befindet. Um den Effekt zu maximieren, solltest du versuchen, so niedrig wie möglich über dem Wasserspiegel zu stehen.
4. Du wirst dann sehen, dass die Höhe eines Objekts, das durch die Erdkrümmung verdeckt ist, für dich berechnet wird. Wenn dir das Objekt zu klein erscheint, kannst du versuchen, den Abstand zwischen Hoch und Niedrig zu vergrößern.

Wenn die Erde flach wäre, würdest du keinen Unterschied zwischen den Objekten auf der anderen Seite des Sees sehen, egal mit welcher Höhendifferenz du sie betrachtest.

Dieses Experiment beweist nicht nur, dass die Erde rund ist, du kannst nämlich auch den Umfang der Erde schätzen. Genau das hat der griechische Mathematiker Eratosthenes um 240 v. Chr. in Alexandria getan. Er wusste, dass es in Assuan, etwa 800 Kilometer weiter südlich, einen Brunnen gibt, in dem das Sonnenlicht am Mittag der Sommersonnenwende den Boden erreichte. Zur gleichen Zeit maß er den Schatten, den ein Stock in Alexandria warf.

Unter der Annahme, dass die Erde rund und die Sonne sehr weit weg ist, und mithilfe der Mathematik, die wir weiter unten erläutern werden, kam er zu dem Schluss, dass der Erdumfang etwa das 50-fache der Entfernung zwischen Alexandria und Assuan beträgt. Das ist zu mehr als 90% am richtigen Ergebnis dran. Ein fantastisches Ergebnis für ein so einfaches Experiment, das vor über 2000 Jahren durchgeführt wurde.

Wenn wir das Dreieck betrachten, das durch den Stock und den Schatten gebildet wird, können wir die Funktion der inversen Tangens (Arkustangens) aus der Trigonometrie verwenden, um den Winkel zwischen dem Stock und dem Sonnenstrahl zu berechnen, indem wir diese Gleichung verwenden:

θ = arctan(Schattenlänge / Stockhöhe).

Dies berechnen wir für beide Orte. Wie hängen diese beiden Winkel mit dem Umfang der Erde zusammen? Die folgende Abbildung hilft uns, diese Frage zu beantworten.

Wir können mit einfacher Geometrie zeigen, dass der Winkel α zwischen den Linien, die durch die Orte A und B und dem Mittelpunkt der Erde gehen, die Differenz der Stockschattenwinkel ist:

α = θ₂ - θ₁

Wir kennen nun die Bogenlänge (Entfernung entlang der Erdoberfläche) zwischen A und B und den Winkel α. Damit können wir die Entfernung mithilfe der Gleichung einfach auf den gesamten Erdumfang hochrechnen:

Erdumfang = Entfernung A → B ∙ (360° / α)

Es ist wichtig zu wissen, dass sich die Entfernung von A nach B ergibt, wenn du nur nach Norden oder Süden reisen könntest (die Nord-Süd-Entfernung). Wir benötigen diese Entfernung, denn nur wenn du nach Norden fährst, wird der Schatten, den der Stock wirft, länger.

Angenommen, Punkt A liegt südlich von Punkt B. Zeichne auf einer Karte eine Linie von Punkt A nach Norden. Zeichne dann eine Linie von Punkt B nach Osten.

Du kannst dieses Experiment auf zwei Weisen durchführen. Entweder reist du eine beträchtliche Strecke nach Norden oder Süden (mehr als 200 Kilometer, je weiter, desto besser) oder du sprichst dich mit jemandem ab, der weit weg wohnt und dir dabei hilft.

Beginnen wir mit der Reisevariante. Am besten machst du das am kürzesten oder längsten Tag des Jahres, da die Tageslänge dann relativ stabil ist. So werden die Fehler bei der Messung des Schattenwinkels an den beiden Standorten reduziert. Hier ist eine Schritt-für-Schritt-Anleitung:

1. Miss die Länge deines Stocks und gib sie in das erste Feld des Rechners ein. Wenn ein Teil des Stocks in der Erde steckt, gib nur die Länge über der Erde an.
2. Miss die Länge des Schattens am Ort A an einem sonnigen Tag, zur Mittagszeit. Gib die Schattenlänge in den Rechner ein, und der Schattenwinkel wird für dich berechnet.
3. Reise zu Ort B und wiederhole Schritt 2.
4. Miss mithilfe einer Karte die Nord-Süd-Entfernung zwischen den beiden Orten und gib diese Zahl in den Rechner ein (siehe Anleitung oben).
5. Der Rechner gibt dir dann eine deine gemessene Schätzung des Erdumfangs und wie nah du an der richtigen Antwort dran warst.

Wenn du einen Freund an einem weiter entfernten Ort hast, umso besser! Das Experiment wird am genausten, wenn ihr beide eure Messungen am selben Tag des selben Jahres zur selben Sonnenzeit durchführt. Befolgt einfach dieselben Schritte. Achtet darauf, dass die beiden Stöcke gleich lang sind und dass ihr den Schatten am selben Tag um 12 Uhr Mittags Ortszeit messt. Diese Option ist viel einfacher und kann an jedem sonnigen Tag des Jahres durchgeführt werden.

Nehmen wir als Beispiel eine Reise von Kopenhagen in Dänemark nach Wien in Österreich (A nach B), mit einer Nord-Süd-Entfernung von etwa 1138 km an. Der Stock ist 0,91 m lang und wir messen eine Schattenlänge von 0,91 m für A. Das bedeutet einen Schattenwinkel von 45°. Dann fahren wir nach B und messen einen Schatten von 1,3 m, was bedeutet, dass der Schattenwinkel hier etwa 55° beträgt.

Gib all diese Zahlen in den Rechner ein und wir erhalten ein Ergebnis von 40 935 km. Das entspricht zu 98% dem tatsächlichen Erdumfang, der zwischen den Polen gemessen wird, nämlich 40 008 km.

Nehmen wir für einen Moment an, dass die Flat Earthers recht haben. Wie funktioniert das obige Beispiel in einem Modell der flachen Erde?

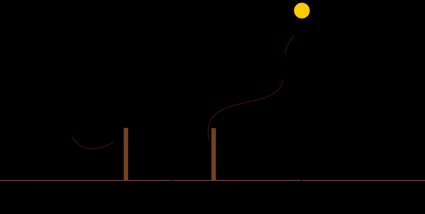
Im Modell der flachen Erde werfen die Stöcke immer noch einen unterschiedlich langen Schatten. Allerdings führt die Trigonometrie zu einem seltsamen Ergebnis. Wenn wir uns auf die obige Abbildung beziehen und die Trigonometrie anwenden, können wir sagen, dass:

d = h ∙ |tan θ₂ - tan θ₁|.

Mit den Winkeln 45° und 60° und 1000 Meilen (≈ 1600 Kilometer) für d ergibt sich, dass die Entfernung h zur Sonne:

h = 1000 / (1,73 - 1) = 1370 Meilen (≈ 2204 Kilometer) ist.

Das scheint SEHR nah zu sein. Das Modell der flachen Erde kann jedoch sagen, dass die Sonne viel kleiner ist, als die Wissenschaft festgestellt hat.

Jetzt können wir die beiden anderen Entfernungen zur Sonne von den beiden Standorten aus berechnen:

R₁ = h / cos θ₁ = 1370 / cos(45°) = 1937 Meilen (≈ 3117 Kilometer)

R₂ = h / cos θ₂ = 1370 / cos(60°) = 2740 Meilen (≈ 4409 Kilometer)

Dieses Ergebnis bedeutet, dass die Sonne bei einer Reise von 1600 Kilometern nach Süden um etwa 40% kleiner geworden sein müsste. Wie du selbst feststellen kannst, scheint die Sonne in Wirklichkeit nicht kleiner zu werden, wenn du nach Süden reist.

Daraus können wir schließen, dass das Modell der flachen Erde falsch ist. Es stimmt nicht mit den Naturbeobachtungen überein. Das ist die entscheidende Eigenschaft jedes wissenschaftlichen Modells. Es muss mit den experimentellen Ergebnissen übereinstimmen.

Die Vorstellung, dass die Erde kugelförmig ist, ist ziemlich alt! Im antiken Griechenland wussten Wissenschaftler und Philosophen schon im 5. Jahrhundert v. Chr. von dieser Tatsache.

Auch in späteren Jahrhunderten war das Kugelmodell weithin akzeptiert und wurde nur am Rande aus rein mythologischen Gründen infrage gestellt: Das scheinbare Wiederaufleben und die Relevanz dieser Theorie in der Neuzeit ist lediglich eine Folge der Veränderung unserer Kommunikationsmethoden.

Um den Umfang der Erde mithilfe von Schatten zu berechnen:

1. Bitte einen Freund oder eine Freundin, der/die auf einem anderen Breitengrad lebt, die gleichen Schritte wie du durchzuführen:
2. Stecke einen Stock mit bekannter Länge senkrecht in den Boden.
3. Miss den Winkel zwischen dem Stab und den Sonnenstrahlen zu einem bestimmten Zeitpunkt des lokalen Tages.
4. Verwende die Formel:
   θ = arctan(Schattenlänge / Stockhöhe).
5. Benutze nun diese Formel für den Erdumfang:
   Erdumfang = Entfernung ∙ (360° / α),
   wobei:
   • Entfernung — die Nord-Süd-Entfernung zwischen den Stöcken ist und
   • α — die Differenz zwischen den zuvor berechneten Winkeln ist.

Um die Krümmung der Erde zu sehen, musst du dich in einer Höhe von etwa 10,5 km befinden. Das ist ungefähr die Reiseflughöhe eines Passagierflugzeugs. Um die Krümmung richtig sehen zu können, brauchst du jedoch einen völlig klaren Horizont (keine Wolken) und ein Sichtfeld von mindestens 60 Grad. Diese beiden Bedingungen sind von den Fenstern eines Flugzeugs aus selten erfüllt, du kannst aber trotzdem versuchen, die Krümmung zu sehen.

Beachte, dass die Krümmung selbst vom Gipfel des Mount Everest aus nicht sichtbar ist!

Um zu beweisen, dass die Erde rund ist, gehe an den Strand! Wenn du ein ausreichend langes Stück Meer vor dir hast, kannst du einfach warten, bis sich ein Schiff der Küste nähert. Du wirst zuerst sehen, wie der obere Teil des Schiffes über dem Horizont auftaucht, dann folgt langsam der Rest des Schiffes.
Da die Erde rund ist, verdeckt ihre Krümmung einen Teil des Schiffes. Der verdeckte Teil wird weniger, je näher dir das Schiff kommt.

Der schwierige Teil ist nun, Skeptiker davon zu überzeugen, dass dies eine endgültige Antwort ist!