Gyllene snittet – Kalkylator

Kalkylatorn för gyllene snittet hjälper dig att räkna ut hur du ska dela upp en sträcka för att få exakt rätt proportioner enligt det gyllene snittet. Innan vi visar hur du räknar ut det gyllene snittet, går vi igenom vad det faktiskt är – och varför det anses vara så harmoniskt och vackert. Här får du all kunskap du behöver!

Vill du lära dig mer om proportioner i allmänhet? Kolla in vå proportion kalkylator 🇺🇸.

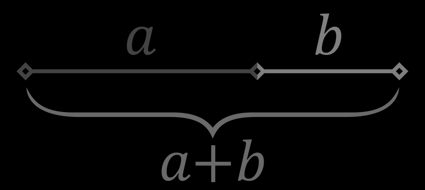
Det gyllene snittet (även känt som gyllene proportionen) uppstår när en sträcka delas i två delar så att förhållandet mellan hela sträckan och den längre delen är samma som förhållandet mellan den längre och den kortare delen. Om den längre delen har längden $a$ och den kortare har längden $b$ så uttrycks formeln för det gyllene snittet så här:

För att räkna ut det gyllene snittets värde behöver vi lösa ekvationen ovan för $a/b$. Det är smidigt att omforma den till:

Till sist behöver vi alltså bara lösa den kvadratiska ekvationen: $x^2-x-1=0$ för $x$. Genom att använda standardmetoder för lösning av andragradsekvationer får vi fram att värdet på det gyllene snittet är: $\frac 12 (1+\sqrt{5})$, vilket är ungefär $1,61803398875...$. Detta tal kallas ofta för det gyllene snittet och betecknas med den grekiska bokstaven $\phi$.

Nu när vi vet vad det gyllene snittet är och hur vi beräknar dess värde, låt oss titta på hur man kan kontrollera om två givna längder följer denna gudomliga proportion.

Följ dessa steg för att ta reda på om två längder är i gyllene snittet:

1. Mät längden på den längre sträckan och kalla den a.
2. Mät längden på den kortare sträckan och kalla den b
3. Beräkna kvoten a/b.
4. Om resultatet är (ungefär) 1,618, då står sträckorna i gyllene förhållande.

Du kan såklart också använda Omnis kalkylator för gyllene snittet. Även en vanlig förhållande kalkylator 🇺🇸 kan hjälpa, men vår kalkylator är helt specialiserad på gyllene snittet, så du hittar inget bättre verktyg!

Omnis kalkylator för gyllene snittet är otroligt enkel att använda. Den innehåller tre fält – ett för varje längd i formeln för gyllene proportion. Det enda du behöver göra är att ange ett av värdena, så räknas de andra två ut automatiskt. Smidigt, eller hur?

En gyllene rektangel är en rektangel vars sidförhållande följer det gyllene snittet, det vill säga att förhållandet mellan längd och bredd är cirka $1,618$. Denna typ av rektangel anses ofta vara den mest estetiskt tilltalande för det mänskliga ögat, och har därför använts flitigt inom konst och design. Vill du enkelt räkna ut sidorna på en gyllene rektangel? Prova vår gyllene rektangeln kalkylator 🇺🇸 – mycket smidigare än att räkna för hand.

Det gyllene snittet har länge haft en särskild betydelse inom både vetenskap och konst – tack vare dess unika egenskaper och naturliga förekomst. Inom matematiken:

• En gyllene rektangel kan delas upp i två mindre gyllene rektanglar och ändå behålla proportionerna.
• Det gyllene snittet har stark koppling till talet 5. Detta tal förekommer i dess definition (φ = (1 + √5)/2) och i femhörningar, där det beskriver förhållandet mellan diagonal och sida.

Inom konsten har gyllene snittet använts i allt från antikens arkitektur till moderna mästare. Exempelvis använde Salvador Dalí detta förhållande i flera av sina verk för att skapa harmoni och balans.

Många historiska och moderna källor menar att det gyllene snittet är vanligt förekommande i naturen. Några ofta nämnda exempel är:

• Tillväxtmönstret hos blad;
• Geometriska mönster på vissa grönsaker och snäckskal;
• Proportionerna i vissa djurs skelett.

Det är dock viktigt att komma ihåg att även om naturen visar många geometriska mönster, så är dessa proportioner inte alltid exakt lika med det gyllene snittet – de kan variera kraftigt och ibland bara ligga nära 1,618.