Calcolatore per la Deviazione Standard della Media di un Campione

Il calcolo della deviazione standard della media di un campione (ovvero la deviazione standard della distribuzione campionaria della media) è un modo eccellente per capire come la dimensione del campione influenzi l'errore delle nostre stime.

Quando la deviazione standard della media viene moltiplicata per un valore critico t, come il punteggio z o la statistica t, otteniamo un margine di errore che ci permette di indicare un intervallo di confidenza della nostra previsione. Pertanto, il calcolo della deviazione standard per la distribuzione campionaria della media indica dove potrebbe trovarsi la media della popolazione.

Prima di tutto, è importante chiarire che questo termine è conosciuto con vari nomi come:

• Deviazione standard della media;
• Deviazione standard della media di un campione;
• Deviazione standard della distribuzione di campionamento delle medie; e
• Deviazione standard della distribuzione di campionamento della media di un campione.

È inoltre fondamentale conoscere alcune definizioni e concetti:

• Statistica — Una stima puntuale o una caratteristica numerica di un campione (ad esempio, la media del campione). È diversa da un parametro, come la media della popolazione;

• Distribuzione di campionamento — La distribuzione di probabilità di una statistica campionata a caso. In altre parole, è la distribuzione di tutti i possibili valori che una statistica potrebbe assumere utilizzando la stessa dimensione del campione; e

• Distribuzione di campionamento della media — Si tratta di un'estensione del concetto precedente. Se hai una popolazione, prelevi infiniti campioni di dimensione n, e tracci le loro medie in un istogramma, ottieni una distribuzione di probabilità. Questa distribuzione di probabilità è quella che chiamiamo distribuzione di campionamento della media e, come qualsiasi altra distribuzione, ha la sua media e la sua deviazione standard.

Il seguente diagramma mostra come generare una distribuzione di campionamento della media. Nella realtà, non utilizziamo solo sei campioni ma un numero quasi infinito (ad esempio, 100 000).

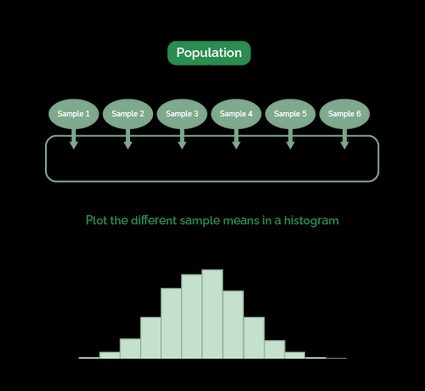
Detto questo, possiamo definire la deviazione standard media come la deviazione standard di una distribuzione di medie (come quella mostrata nell'ultimo diagramma). Inoltre, la media di questa distribuzione di campionamento è uguale alla media della popolazione.

Ora che conosci il concetto, vediamo come calcolare la deviazione standard della media campionaria.

La differenza tra una distribuzione campionaria e una distribuzione di campionamento è:

• Distribuzione di campionamento — È il termine che sentiamo di solito. Si riferisce alla distribuzione di probabilità di una statistica campionata a caso. La distribuzione campionaria della media ne è un esempio; e
• Distribuzione campionaria — Si riferisce alla distribuzione delle osservazioni all'interno di un solo campione. Ogni distribuzione campionaria possiede una media, che contribuisce a formare la distribuzione di campionamento.

La formula per trovare la deviazione standard della media di un campione è:

σ_X̄ = σ/√n,

dove:

• σ_X̄  — Deviazione standard della media del campione;
• σ — Deviazione standard della popolazione; e
• n — Dimensione del campione.

In precedenza abbiamo detto che se conosciamo la media della distribuzione campionaria (μ_X̄), conosciamo anche la media della popolazione (μ), poiché sono uguali (μ_X̄ = μ). In pratica, non conosciamo mai μ_X̄, ma possiamo stimarla utilizzando la media del campione (X̄).

σ_X̄ indica come X̄ si approssima a μ. Più σ_X̄ è piccolo, più μ si avvicina alla nostra stima. Poiché σ è costante, aumentare la dimensione del campione è l'unico modo per diminuire σ_X̄. Pertanto, aumentare n è un modo per ridurre l'errore di campionamento 🇺🇸 delle nostre stime.

Sappiamo che la media e la deviazione standard dell'altezza della popolazione femminile americana adulta è di circa μ = 161,3 cm e σ = 7,1 cm. Ora, supponiamo di prendere a caso campioni di 100 donne e di rilevare ogni volta la loro altezza media. Qual è la deviazione standard della media del campione?

Per conoscere la risposta, segui questi passaggi:

1. Inserisci 7,1 nel campo della deviazione standard della popolazione;
2. Inserisci 100 nel campo della dimensione del campione; e
3. Ecco fatto. La risposta dovrebbe essere 0,71. Pertanto, la deviazione standard delle distribuzioni di campionamento della media è n = 100 è 0,71.

Puoi verificare i risultati utilizzando la formula: $σ_{\bar X} = \frac{σ}{\sqrt{n}} = \frac{7,1}{\sqrt{100}} = 0,\!71$.