Calcolatore di Velocità Angolare

Questo calcolatore di velocità angolare è uno strumento semplice da usare che fornisce una risposta immediata alla domanda "Come si trova la velocità angolare?". Nel testo troverai diverse formule di velocità angolare, imparerai a conoscere le diverse unità di misura della velocità angolare e, infine, potrai stimare la velocità angolare della Terra!

Ti chiedi mai qual è la relazione tra velocità angolare e frequenza angolare? O in quali contesti si applica la velocità angolare? Continua a leggere per scoprirlo e specializzarti nel movimento circolare.

La velocità angolare descrive il movimento rotatorio dei corpi. Misura la velocità con cui i corpi si muovono intorno a un centro di rotazione. Possiamo pensare a due diversi tipi di rotazione. La prima descrive il movimento del centro di massa di un dato oggetto intorno a un punto specifico nello spazio, che possiamo definire come l'origine. Alcuni esempi sono i pianeti che si muovono intorno al Sole, o un'auto che prende un'uscita in autostrada.

La seconda riguarda la rotazione del corpo intorno al proprio centro di massa. Sicuramente avrai visto un giocatore di basket che fa girare una palla sul dito.

In generale, possiamo dire che più veloce è il movimento, maggiore è la velocità angolare. Passiamo alle equazioni della velocità angolare descritte nella prossima sezione per definire alcuni valori specifici.

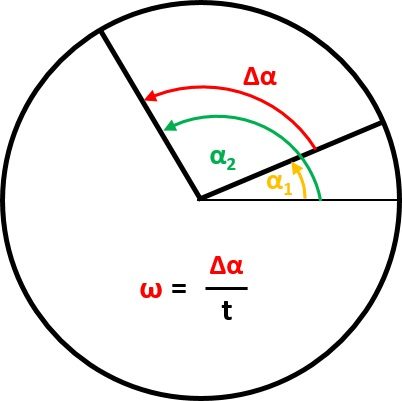
Questo calcolatore di velocità angolare utilizza due diverse formule a seconda dei parametri inseriti.

La prima equazione della velocità angolare è analoga all'equazione della velocità lineare:

dove:

• $\alpha_1$ e $\alpha_2$ — Angoli su una circonferenza;
• $\Delta\alpha$ — Differenza tra gli angoli $\alpha_1$ e $\alpha_2$; e
• $t$ — Periodo di tempo in cui avviene la variazione dell'angolo.

Come puoi vedere, per la velocità normale esiste un rapporto tra lo spostamento di posizione in un periodo, mentre in questo caso utilizziamo l'angolo invece della distanza.

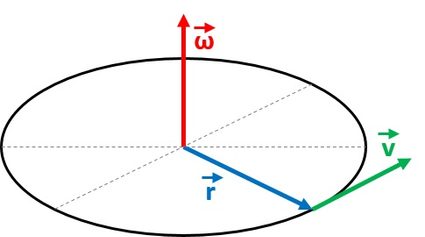
Possiamo ricavare la seconda formula della velocità angolare dalla relazione tra la velocità lineare e il raggio utilizzando il prodotto vettoriale, che è:

Possiamo riscrivere questa espressione per ottenere l'equazione della velocità angolare:

dove:

• $\vec{n}$ — Vettore; e
• $|r|$ — Valore assoluto del raggio.

In realtà, la velocità angolare è uno pseudovettore la cui direzione è perpendicolare al piano del movimento rotatorio.

Esistono diverse unità di misura della velocità angolare. Ecco quelle che utilizziamo nel nostro calcolatore di velocità angolare:

• rad/s o radianti al secondo — La definizione deriva direttamente dalla prima formula della velocità angolare. Indica l'ampiezza della rotazione (o dell'angolo) che il corpo compie in un determinato tempo;

• RPM o giri al minuto — È l'unità di misura che si trova più spesso nelle applicazioni pratiche. Utilizzandola, è possibile descrivere la velocità di rotazione di una ruota o di un motore. Puoi facilmente immaginare la differenza tra 10 e 100 RPM; e

• Hz o hertz — Le stesse unità utilizzate per la frequenza, ma raramente utilizzate nel contesto della velocità angolare. È in qualche modo simile agli RPM, in quanto ci dice quante rotazioni complete vengono effettuate in un determinato tempo. La differenza gli RPM utilizzano il minuto come unità di base, mentre gli hertz utilizzano il secondo.

Naturalmente, tutte queste unità di misura della velocità angolare si convertono tra loro utilizzando le seguenti relazioni:

1 RMP = 0,10472 rad/s = 0,01667 Hz,

Oppure il contrario:

1 Hz = 6,283 rad/s = 60 RPM

Guarda la definizione di frequenza angolare:

dove:

• $f$ — Frequenza.

Come possiamo vedere, la frequenza angolare viene indicata con la stessa lettera che la velocità angolare. Inoltre, l'unità di misura della frequenza angolare è rad/s, esattamente come quella della velocità angolare. Quindi potrebbe sorgere la domanda: "Qual è la differenza tra velocità angolare e frequenza angolare?".

La risposta è relativamente semplice. La relazione tra frequenza angolare e velocità angolare è analoga a quella tra velocità media e velocità. La prima è una magnitudine della seconda, o in altre parole, la frequenza angolare è uno scalare, mentre la velocità angolare è uno (pseudo)vettore.

Di solito si usa la frequenza angolare quando si parla di un movimento armonico, di cui un esempio è un semplice pendolo. Come puoi immaginare, il movimento non deve essere rappresentato da una rotazione semplice, ma da un movimento che ritorna periodicamente alla stessa posizione. La velocità angolare, invece, è strettamente legata al movimento intorno a un punto. Pertanto, possiamo dire che la frequenza angolare è una quantità più generale e possiamo utilizzarla per descrivere un'ampia gamma di problemi fisici, mentre la velocità angolare analizza solo il movimento rotatorio.

Che ne dici di utilizzare il nostro calcolatore di velocità angolare? Stimiamo la velocità angolare della Terra! Per prima cosa, consideriamo la velocità di rotazione. Sappiamo che la Terra compie una rotazione completa, rispetto alle stelle lontane, in circa 23 h 56 min e 4 s, ovvero circa 23,934 h. L'intera rotazione corrisponde all'angolo 2π rad, quindi la velocità angolare risultante è:

o $7,\!292 \times 10^{-5}\ \rm rad/s$ utilizzando la notazione scientifica.

Ora che conosciamo la velocità angolare di rotazione della Terra, possiamo valutare la sua velocità lineare all'equatore. Per farlo, abbiamo bisogno del raggio della Terra, che è pari a circa 6371 km. L'unica cosa che dobbiamo fare è inserire i valori nella seconda formula della velocità angolare:

Per calcolare la velocità lineare rispetto al centro della Terra, tutto ciò che devi fare è moltiplicare questo risultato per il coseno della latitudine della tua città.

A proposito, hai mai pensato al motivo per cui di solito i razzi vengono lanciati da spazioporti situati vicino all'equatore e non ai poli? Ebbene, una spinta di 500 m/s all'inizio è una frazione considerevole della velocità finale. Quindi, spostare il punto di partenza il più vicino possibile all'equatore riduce la quantità di carburante necessaria per accelerare il razzo.

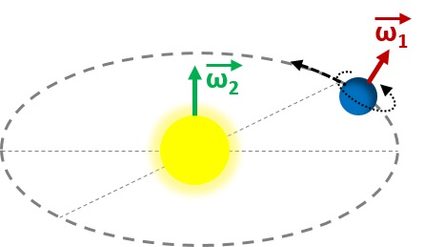
Dopodiché, possiamo chiederci ancora una volta come trovare la velocità angolare della Terra, ma questa volta quella orbitale. Tutti i calcoli sono analoghi, ma dobbiamo cambiare il tempo da 23,943 h a un anno, ovvero circa 365,25 giorni. La variazione dell'angolo è la stessa, la rivoluzione completa.

La velocità lineare della Terra rispetto al Sole (per il raggio medio pari a $\small 1,\!496\!\times\!10^8\ \rm km$) è:

Ci stiamo muovendo molto velocemente, vero?

Molteplici quantità fisiche sono correlate alla velocità angolare. Eccone alcune:

1. Accelerazione angolare — Descrive il modo in cui la velocità angolare cambia nel tempo. Maggiore è la differenza tra le velocità angolari, maggiore è il l'accelerazione angolare. Non esitare a verificarne il funzionamento pratico con il nostro calcolatore di accelerazione angolare 🇺🇸;

2. Energia cinetica rotazionale — Misura l'energia di un moto circolare. Com'è solito con l'energia cinetica, la dipendenza dalla velocità (angolare) è quadratica;

3. Forza centripeta — È la forza che ti fa girare o ruotare in moto circolare. In un'auto che gira, gli pneumatici esercitano questa forza. La tendenza a mantenere il moto rettilineo (primo principio di Netown) è chiamata inerzia o forza centripeta, anche se non è una forza reale;

4. Effetto Coriolis — Fa sì che gli oggetti ruotino se si trovano su un corpo rotante (ad esempio, sulla Terra) invece di muoversi in linea retta; e

5. Sistema di pulegge — Non si tratta di una grandezza fisica, ma di un interessante dispositivo che riguarda la velocità angolare. Il sistema più semplice consiste in due pulegge, solitamente con circonferenze o raggi diversi. Sono collegate da un cinghia, quindi le loro velocità lineari sono identiche, ma poiché sono di dimensioni diverse, le loro velocità angolari cambiano proporzionalmente.

   Essendo al corrente di tutto ciò e disponendo di un motore con una velocità di rotazione ben definita, possiamo impostare la velocità angolare dell'elemento di uscita con buona precisione semplicemente regolando le sue dimensioni.

Alcune regole fondamentali ci parlano delle quantità che si conservano nei sistemi isolati. Le più conosciute sono la conservazione dell'energia e la conservazione del momento. Insieme a esse, esiste anche la conservazione del momento angolare. Se pensiamo a due momenti nel tempo, possiamo descrivere questa regola come:

dove:

• $I_1$ — Momento d'inerzia di massa iniziale; e
• $I_2$ — Momento d'inerzia di massa finale.

Queste due quantità descrivono la distribuzione di massa rispetto ai rispettivi centri di rotazione.

Possiamo notare che se il momento d'inerzia aumenta, la velocità angolare diminuisce e viceversa. Quali sono le conseguenze di questo fenomeno?

Immaginiamo che tu faccia pattinaggio artistico. Quando giri, possiedi una certa velocità angolare. Se le tue braccia sono aperte, il momento di inerzia di massa è relativamente grande. Poi, avvicini le braccia al resto del corpo. Di conseguenza, il tuo momento d'inerzia diminuisce e, poiché il momento angolare complessivo deve essere conservato, la tua velocità angolare aumenta; ciò significa che girerai più velocemente! Non si tratta di magia — è pura fisica!

Se non puoi o non ti piace pattinare, puoi provare a verificare la regola con una normale sedia girevole. Ricorda però che la sicurezza è al primo posto! Assicurati che ci sia spazio sufficiente per fare questo esperimento. Dopodiché, inizia a girare e osserva come cambia la tua velocità angolare quando muovi le braccia avanti e indietro. Inoltre, puoi aumentare l'effetto utilizzando dei manubri. In questo modo potrai combinare esercizio e divertimento!