Calcolatore per la Terra Piatta o Rotonda

Qual è il modo migliore per conoscere il mondo? Proporre una teoria e cercare di dimostrarla con le osservazioni (scienza)? Oppure inventare cose e ignorare fatti evidenti (scemenza)? Qui a Omni, tendiamo a pensare che la prima opzione vada piuttosto bene. Ci ha portato sulla Luna, non è vero? — A proposito, l'ha fatto per davvero!

Per celebrare la Giornata Mondiale della Scienza per la Pace e lo Sviluppo, che si tiene ogni 10 novembre, abbiamo creato un calcolatore per aiutarti a combattere contro le fandonie, le mezze verità e le sciocchezze, a favore della scienza, dell'osservazione e dell'apertura mentale.

Il calcolatore di Omni per la Terra piatta o rotonda include esperimenti che aiutano a dimostrare che la Terra è davvero rotonda. Non preoccuparti, non dovrai costruire il tuo razzo per andare nello spazio a verificare (o calcolare il suo impulso e il suo momento 🇺🇸 o la sua energia cinetica 🇺🇸).

Ti proponiamo tre esperimenti relativamente semplici da provare:

• Ombre di un bastone — Usa la lunghezza delle ombre proiettate da un bastone in diversi punti per stimare la circonferenza della Terra;
• Doppio tramonto — Cambiando il tuo punto di vista dal suolo, potrai vedere il tramonto due volte. Il nostro calcolatore ti dice quanta parte del secondo tramonto vedrai; e
• Oggetti che scompaiono — Nascondi gli oggetti dietro la curvatura della Terra cambiando l'altezza del tuo punto di vista. Questo calcolatore ti mostra l'altezza di un oggetto che puoi far sparire.

Prima di passare agli esperimenti, vediamo brevemente perché le persone credono nella Terra piatta e il modello di mondo che propongono.

Incredibilmente, nel paese più ricco e tecnologicamente sviluppato del mondo, un abitante su sei non è sicuro che la Terra sia rotonda 🤔. Naturalmente, il paese sono gli Stati Uniti e la convinzione che la Terra sia piatta potrebbe derivare dalla sua cultura altamente individualista e dalla sfiducia nelle autorità, nelle istituzioni e negli esperti.

I terrapiattisti sembrano guardare il mondo da soli, senza fare riferimento agli oltre 2000 anni di scoperte umane. Wow, si stanno perdendo tutto. Inoltre, sono estremamente diffidenti nei confronti di qualsiasi fatto che non abbiano verificato personalmente. Altro che problemi di fiducia...

Quindi affrontano sfide straordinarie per dimostrare che la Terra è piatta quando ci sono azioni semplici che potrebbero compiere per dimostrare che la Terra è rotonda. Ecco alcuni esempi:

• "Mad" Mike Hughes ha costruito i suoi razzi a vapore per volare a un'altezza di 550 metri per fotografare la mancanza di curvatura del deserto del Mojave. Purtroppo, per vedere la curvatura della Terra bisogna salire almeno a 11 000 metri di altezza. Sfortunatamente, è deceduto nel febbraio del 2020 in un volo di razzo fallito;
• La star di YouTube Logan Paul aveva intenzione di visitare l'Antartide per trovare il bordo della Terra piatta. Tuttavia, il viaggio non si è svolto a causa della pandemia COVID-19 e della mancanza di strutture mediche per far fronte a eventuali emergenze; e
• Il rapper B.o.B ha cercato di finanziare in crowdfunding il lancio del suo satellite per verificare la presenza della Terra piatta. È riuscito a raccogliere solo 6883 dollari del suo obiettivo di 1 milione di dollari. Va beh, non importa. Forse potrebbe invece provare i nostri semplici esperimenti a basso costo.

Questa vignetta di Tom Fonder riassume bene i terrapiattisti.

Nel modello della Terra piatta, il mondo è un disco (simile agli ingranaggi utilizzati per la riduzione degli ingranaggi) con il polo nord al centro. Intorno al bordo del disco si trovano il ghiaccio e la neve del "polo sud". Questo forma una barriera di ghiaccio, presumibilmente per impedire all'acqua degli oceani di cadere dal disco nello spazio.

Lo spessore del disco della Terra piatta non è chiaro. Tuttavia, la massa coinvolta deve essere molto inferiore a quella di una Terra rotonda, quindi la Terra non sarebbe in grado di trattenere la sua atmosfera. Forse c'è una cupola trasparente sopra la Terra, che ne impedisce la fuoriuscita.

Il modello tradizionale della Terra piatta prevede che il sole sia posizionato sopra il disco, girando nel cielo come la giostrina di un bambino e a una distanza molto più ravvicinata. Questo però non spiega i tramonti e le albe. Per la nostra salute mentale, immaginiamo che il disco giri come una moneta rispetto al sole. In questo modo, almeno, si otterrebbero l'alba e il tramonto (qualcosa che anche l'animale più semplice potrebbe osservare). Tuttavia, non ci sarebbero fusi orari, poiché l'alba e il tramonto sarebbero alla stessa ora in tutto il mondo.

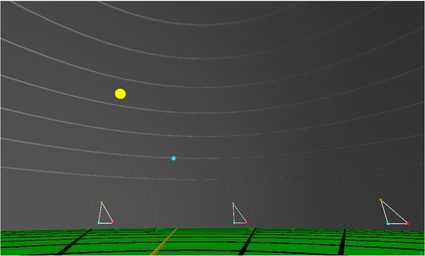
Questo è il problema principale del modello della Terra piatta. È pieno di incongruenze e osservazioni inspiegabili. Ad esempio, perché fa freddo sia al centro che ai bordi del disco?

Torniamo a un modo di pensare più scientifico e introduciamo il primo esperimento.

Questo primo esperimento può essere molto semplice da realizzare. Muoviti verso l'alto abbastanza velocemente da precedere l'ombra proiettata dall'orizzonte. Sarai in grado di vedere parte del tramonto due volte! Se osservi questo, allora la Terra è davvero rotonda. Questo esperimento ti permetterà di calcolare quanta parte di un secondo tramonto potrai vedere e quanto a lungo potrai far durare un tramonto.

Cosa vedresti se la Terra fosse piatta? Nessun secondo tramonto 😭. Non importa quanto in alto o quanto velocemente ti sposterai dalla superficie di una Terra piatta, non vedrai più il sole fino all'alba.

In una Terra rotonda, quando il sole tramonta, immagina che l'ombra proiettata dall'orizzonte terrestre venga verso di te e risalga lungo la tua altezza. Se riesci a precedere quest'ombra muovendoti abbastanza velocemente verso l'alto, potrai vedere di nuovo il tramonto. Diamo un'occhiata alla matematica.

Questo documento ci fornisce un'equazione che mette in relazione il tempo con l'altezza dell'ombra:

t = 8 × √h,

dove t è il tempo che ci impiega l'ombra a spostarsi in altezza della quantità h. Possiamo mettere in relazione h con la differenza di altezza tra due altezze e t con il tempo necessario per spostarsi verso l'alto. Poiché non possiamo spostarci istantaneamente dall'altezza inferiore a quella superiore, dobbiamo considerare il tempo di spostamento. Infine, per trovare la quantità di un secondo tramonto che possiamo vedere di nuovo, dobbiamo conoscere la durata del tramonto. Abbiamo quindi questa equazione per la percentuale del secondo tramonto che potrai osservare:

Percentuale del doppio tramonto = 100 × (1 - ((Durata del tramonto - t - Tempo di viaggio) / Durata del tramonto)).

Esistono alcuni modi per rivedere il sole subito dopo il suo tramonto, in misura variabile. Il calcolatore di Omni per la Terra piatta o rotonda ti dirà quanta parte del secondo tramonto sarai in grado di osservare. Vediamo tre idee che ci sono venute in mente.

1. Sdraiati, alzati in piedi

Questa idea è la più semplice in termini di attrezzatura. Hai solo bisogno di un luogo in cui puoi vedere il sole che tramonta sul mare o su un terreno molto piatto (come un deserto). Anche un bel cielo senza nuvole ti aiuterà. Tutto ciò che devi fare è guardare il tramonto sdraiato. Quando non riesci più a vedere il sole, alzati immediatamente il più velocemente possibile. Dovresti riuscire a vedere di nuovo una piccola parte della parte superiore del sole.

Ecco come si utilizza il calcolatore per calcolare con precisione la quantità:

1. Seleziona la località più vicina a te o inserisci manualmente la durata del tramonto nel luogo in cui ti trovi;

2. Inserisci l'altezza iniziale più bassa dell'altezza dei tuoi occhi. In questo caso, quando sei sdraiato. Consigliamo circa 20 cm;

3. Inserisci il tempo che ci impiegherai a raggiungere l'altezza superiore. Noi pensiamo che ci voglia circa mezzo secondo, ma cronometrati lo stesso per controllare;

4. Inserisci l'altezza finale del tuo sguardo quando sei in piedi. Puoi misurarla sottraendo dalla tua altezza la distanza tra la sommità della testa e gli occhi; e

5. A questo punto vedrai la percentuale di sole che riuscirai a vedere di nuovo. Vuoi vederne di più? Prova a cambiare i valori nel calcolatore o vai alle varianti più avanzate dell'esperimento qui sotto.

Con questo metodo dovresti riuscire a vedere circa il 5% del secondo tramonto.

2. Sali velocemente su un grattacielo

Per vedere meglio il secondo tramonto, dovrai andare più in alto e più velocemente per anticipare l'ombra dell'orizzonte. Un grattacielo con un ascensore veloce è una buona opzione. Questo fenomeno è stato osservato presso l'hotel Burj Khalifa di Dubai.

Per selezionare i valori di inserimento per questo grattacielo, scegli "ascensore del grattacielo dell'hotel Burj Khalifa" dall'elenco delle idee. Se vuoi provare con un altro edificio, regola i valori di inserimento di conseguenza.

Dovresti essere in grado di vedere di nuovo un enorme 88% del tramonto, raddoppiando così la durata. Se sei un amante del tramonto, questa è la cosa da fare.

3. Drone con fotocamera

Un'altra idea è quella di utilizzare un drone di buona qualità dotato di telecamera per i filmati in diretta. Abbiamo trovato un drone che può raggiungere 1000 metri in 200 secondi. Se selezioni "drone" dall'elenco delle idee, vedrai che con questo metodo dovresti vedere circa un terzo del tramonto.

Verifica la velocità e l'altezza del tuo drone e regola i valori del calcolatore di conseguenza.

In questo esperimento nasconderemo parte di un oggetto dietro la curvatura della Terra. Dovrai trovare uno specchio d'acqua in cui la riva lontana sia distante almeno 2 km e deve essere una bella giornata calma e senza vento.

Inoltre, per evitare l'effetto miraggio della luce [rifrazione], fai l'esperimento al mattino quando è fresco. Questo è anche il motivo per cui ti sconsigliamo di usare un deserto — l'effetto miraggio ti impedirà di vedere gli oggetti sulla riva lontana in modo sufficientemente chiaro.

In questo video di YouTube, il ragazzo ha fatto sparire un camion a 7 km di distanza sul lato opposto di un lago abbassando la sua telecamera più vicino al terreno.

In alternativa, anche un parco eolico in alto mare è una buona opzione, come dimostra questa fotografia:

Nota che più un mulino a vento è lontano, più è nascosto. Questo è lo scopo dell'esperimento — calcolare per quanto tempo è possibile nascondere un oggetto lontano dietro la curvatura della Terra.

In questo esperimento, inizieremo da un punto di vista alto e poi scenderemo a un punto di vista basso per oscurare un oggetto lontano. In termini matematici, troveremo quanto è nascosto nelle visuali alte e basse e calcoleremo la differenza.

Per calcolare l'altezza oscurata, dobbiamo prima conoscere la distanza dall'orizzonte. Questa è data da questa equazione:

a = √[(r + h)² - r²],

dove:

• a — distanza dall'orizzonte;
• h — livello del punto di vista dal suolo; e
• r — raggio della Terra, pari a 6371 km.

Quindi inseriamo il risultato in una seconda equazione che calcola la quantità di oggetto oscurato, x, se visto da un'altezza zero:

x = √(a² - 2ad + d² + r²) - r.

La differenza tra i due valori di x è l'altezza dell'oggetto che possiamo far scomparire cambiando il nostro punto di vista.

Ok, hai trovato un luogo eccellente, ad esempio un lago con la riva a pochi chilometri di distanza. Per vedere gli oggetti sulla riva lontana, avrai bisogno di un buon binocolo. Meglio ancora, una videocamera con un potente obiettivo zoom. In questo modo potrai anche registrare l'esperimento, come nel video qui sopra.

Per avere una visione stabile attraverso il binocolo o la videocamera, è consigliabile montarli su un treppiede. L'utilizzo di un treppiede ti permette anche di misurare con precisione le due altezze.

Ecco come si utilizza il calcolatore per capire le dimensioni dell'oggetto che potresti far sparire dietro la curvatura della Terra:

1. Misura la distanza dalla riva più lontana del lago. Per farlo puoi utilizzare una mappa cartacea o la funzione di misurazione di Google Maps. Inserisci la distanza nella variabile "Distanza dall'oggetto" del calcolatore;

2. Misura l'altezza da terra del tuo occhio in piedi o della tua fotocamera quando è in posizione elevata. Inserisci questa altezza nel campo successivo;

3. Fai lo stesso quando sei sdraiato o la tua fotocamera è in posizione di altezza ridotta. Per massimizzare l'effetto, cerca di abbassarti il più possibile al livello dell'acqua; e

4. Vedrai che l'altezza di un oggetto oscurato dalla curvatura della Terra verrà calcolata per te. Se ti sembra troppo piccolo da vedere, prova ad aumentare l'altezza e a diminuire l'altezza.

Se la Terra fosse piatta, non vedresti alcuna differenza tra gli oggetti che si trovano sul lato opposto del lago, indipendentemente dalla loro altezza dal suolo.

Questo esperimento non solo dimostra che la Terra è rotonda, ma permette anche di stimare la circonferenza della Terra. Questo è esattamente ciò che fece il matematico greco Eratostene ad Alessandria, intorno al 240 a.C. Sapeva che ad Assuan, a circa 800 km a sud, c'era un pozzo dove la luce del sole raggiungeva il fondo a mezzogiorno del solstizio d'estate. Allo stesso tempo, misurò l'ombra proiettata da un bastone ad Alessandria.

Partendo dal presupposto che la Terra fosse rotonda e il sole fosse lontano, e utilizzando i calcoli che vedremo di seguito, concluse che la circonferenza della Terra era circa 50 volte la distanza tra Alessandria e Assuan. Cioè meno del 10% della risposta corretta. Un risultato fantastico per un esperimento così semplice eseguito oltre 2000 anni fa.

Osservando il triangolo formato dal bastone e dall'ombra, possiamo utilizzare la funzione trigonometrica della tangente inversa per calcolare l'angolo tra il bastone e il raggio di luce solare, utilizzando l'equazione:

θ = arctan(lunghezza dell'ombra / altezza del bastone).

Quindi facciamo così per le due posizioni. Come si relazionano questi due angoli con la circonferenza della Terra? La figura seguente ci aiuterà a rispondere a questa domanda.

Utilizzando un po' di geometria, possiamo dimostrare che l'angolo α tra le linee che passano per le posizioni A e B e il centro della Terra è uguale alla differenza degli angoli dell'ombra dei bastoni:

α = θ₂ - θ₁.

Ora conosciamo la lunghezza dell'arco (distanza lungo la superficie della Terra) tra A e B e l'angolo α. Questo ci permette di scalare la distanza all'intera circonferenza della Terra, utilizzando l'equazione:

Circonferenza della Terra = Distanza A → B × (360° / α).

È importante notare che la distanza da A a B dovrebbe essere la distanza che si avrebbe se si potesse viaggiare solo verso nord o verso sud (la distanza nord-sud). Abbiamo bisogno di questa distanza perché solo quando si viaggia verso nord l'ombra proiettata dal bastone si allunga.

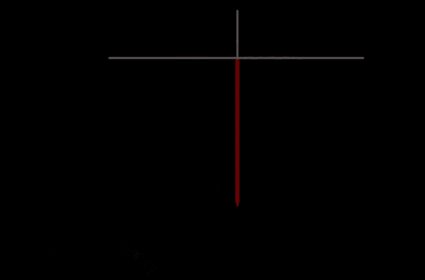
Supponendo che il punto A sia a sud del punto B, traccia su una mappa una linea verso nord dal punto A. Poi traccia una linea verso est dal punto B. La distanza nord-sud è la lunghezza dal punto A al punto in cui le due linee disegnate si incrociano.

Ci sono due modi principali per provare questo esperimento. Puoi viaggiare a una distanza considerevole verso nord o verso sud (più di 160 km, ma più lontano è, meglio è) o collaborare con qualcuno che vive lontano per aiutarti.

Cominciamo con l'opzione del viaggio. La cosa migliore è tentare di farlo durante il giorno più corto o più lungo dell'anno, in quanto la lunghezza del giorno è relativamente stabile. In questo modo si ridurranno gli errori nell'angolo d'ombra misurato nelle due località. Ecco le istruzioni passo passo:

1. Misura la lunghezza del tuo bastone. Dovrai inserirla nel primo campo di input del calcolatore. Se una parte del bastone è nel terreno, includi solo la lunghezza in superficie;

2. Misura la lunghezza dell'ombra nella posizione A a mezzogiorno. Se non è una giornata di sole, aspetta di averne una. Inserisci la lunghezza dell'ombra nel calcolatore e l'angolo dell'ombra verrà calcolato per te;

3. Raggiungi la posizione B e fai come al punto 2;

4. Utilizzando una mappa, misura la distanza nord-sud tra le due località e inserisci questa cifra nel calcolatore (vedi le istruzioni precedenti); e

5. Riceverai quindi una risposta alla tua stima della circonferenza della Terra e quanto ti sei avvicinato alla risposta reale.

Se hai un amico in un'altra posizione che ti aiuta, i passaggi sono praticamente gli stessi. Assicurati che i due bastoni siano della stessa lunghezza e che misuri l'ombra a mezzogiorno ora locale dello stesso giorno. Questa opzione è molto più semplice e può essere eseguita in qualsiasi giorno di sole dell'anno.

Per fare un esempio, andiamo da Napoli a Copenhagen (da A a B), coprendo una distanza nord-sud di circa 1650 km. Il bastone è lungo 0,91 m e misuriamo un'ombra lunga 0,91 m ad A. Questo significa un angolo d'ombra di 45°. Poi ci spostiamo in B e misuriamo un'ombra di 1,5 m, il che significa che l'angolo d'ombra è di circa 60°.

Inserendo tutte queste cifre nel calcolatore, otteniamo un risultato di 39 600 km. Si tratta di meno del 4% di margine della circonferenza reale misurata tra i poli, pari a 40 008 km.

Immaginiamo che i terrapiattisti abbiano ragione per un momento. Come funziona l'esempio precedente in un modello di Terra piatta?

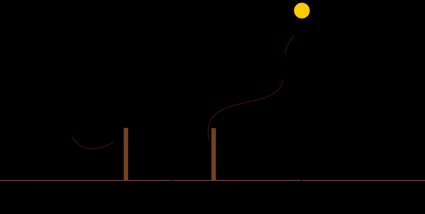
In un modello di terra piatta, i bastoni continueranno a proiettare un'ombra di lunghezza diversa. Tuttavia, il risultato di un po' di calcoli trigonometrici porta a uno strano risultato. Facendo riferimento al diagramma precedente e applicando i sudetti calcoli, possiamo dire che:

d = h × (tan θ₂ - tan θ₁).

Usando gli angoli 45° e 60° e 1600 km per d, vediamo che la distanza dal sole h è

h = 1609/ (1,73 - 1) = 2204 km.

Questo dato sembra molto vicino. Tuttavia, il modello della Terra piatta può affermare che il sole è molto più piccolo di quanto la scienza abbia concluso.

Ora possiamo calcolare le altre due distanze dal sole dalle due località:

R₁ = h / cos θ₁ = 2204 / cos(45°) = 3117 km,

R₂ = h / cos θ₂ = 2204 / cos(60°) = 4409 km.

Questo risultato significa che viaggiando verso sud per circa 1600 km, il sole dovrebbe rimpicciolirsi del 40% circa. In realtà, come puoi verificare tu stesso, il sole non sembra rimpicciolirsi man mano che si procede verso sud.

Pertanto, possiamo concludere che il modello della Terra piatta è sbagliato. Non è in accordo con l'osservazione. Questa è la proprietà fondamentale di qualsiasi modello scientifico. Deve essere in accordo con i risultati sperimentali.

Sappiamo che la Terra è rotonda da molto tempo ormai! Nell'Antica Grecia, scienziati e filosofi erano consapevoli di questo fatto già nel V secolo a.C.

Anche nei secoli successivi, il modello sferico era più ampiamente accettato e solo marginalmente messo in discussione al di fuori di motivazioni puramente mitologiche; l'apparente rinascita di questa teoria e la sua rilevanza nei tempi moderni è solo una conseguenza del cambiamento dei nostri metodi di comunicazione.

Come si calcola la circonferenza della Terra utilizzando le ombre:

1. Chiedi a un amico che vive a una latitudine diversa di eseguire gli stessi passi che hai fatto tu;

2. Pianta verticalmente un bastone di lunghezza nota nel terreno;

3. Misura l'angolo tra il bastone e i raggi del sole a una determinata ora del giorno locale;

4. Usa la formula:
   θ = arctan(Lunghezza dell'ombra / Altezza del bastone); e

5. Ora usa questa formula per la circonferenza della Terra:
   Circonferenza della Terra = Distanza × (360° / α),
   dove:

   • Distanza è la distanza nord-sud tra i bastoncini; e
   • α è la differenza tra gli angoli calcolati in precedenza.

Per vedere la curvatura della Terra, devi trovarti a un'altitudine di circa 10,5 km. Si tratta dell'altitudine di crociera di un aereo passeggeri. Tuttavia, per vederlo bene, è necessario un orizzonte completamente chiaro (senza nuvole) e un campo visivo di almeno 60 gradi. Entrambe queste condizioni sono raramente soddisfatte dai finestrini dell'aereo, ma puoi provarci.

Inoltre, nota che la curvatura non è visibile nemmeno dalla cima del Monte Everest!

Per dimostrare che la Terra è rotonda, vai in spiaggia! Se davanti a te c'è un tratto di mare abbastanza lungo, puoi semplicemente aspettare che una nave si avvicini alla costa. Vedrai prima la sua parte superiore apparire sopra l'orizzonte, seguita lentamente dal resto della nave.
Poiché la Terra è rotonda, la sua curvatura copre parte della nave. La parte coperta si riduce man mano che la nave si avvicina a te.

Ora, la parte difficile è convincere gli scettici che questa è una risposta definitiva!