Calcolatore per il Confronto delle Pizze (Versione Precedente)

Vedi il calcolatore per le dimensioni della pizza! 🇺🇸, la versione più recente del calcolatore per il confronto della pizza 🍕

Quante volte ti chiedi se sia meglio prendere 2 pizze medie o una sola pizza grande? O cerchi "confronto pizza" su Google, sperando di fare la scelta giusta per soddisfare le tue voglie? Probabilmente è capitato a molti. Le pizzerie di solito ti dicono il diametro della pizza, ma noi non mangiamo il diametro. Non mangiamo nemmeno la circonferenza. Quello che mangiamo è l'area della pizza. Si tratta di un calcolo matematico molto elementare che ruota attorno all'equazione Area = raggio² × π, ma spesso abbiamo troppa fretta o non riusciamo a fare i calcoli a mente. Ecco perché abbiamo creato questo calcolatore per confrontare le dimensioni della pizza: per risolvere questi problemi una volta per tutte. Continua a leggere per imparare la matematica che sta alla base delle pizze e per visualizzare le diverse crescite della circonferenza e dell'area in un efficace confronto delle dimensioni della pizza da 30 centimetri (12 pollici). Continua a leggere per imparare:

• Come svolgere un confronto matematico della pizza;
• Perché usiamo una pizza da 30 centimetri nel confronto delle dimensioni; e
• Come si utilizza il nostro calcolatore per il confronto delle dimensioni della pizza.

Qual è la geometria di una pizza? Tutto sta nei cerchi. Il cerchio è una forma elementare, probabilmente la più semplice o la più complessa che si possa immaginare. Composti da un numero infinito di lati disposti a distanza costante da un punto centrale, i cerchi richiedono alcune formule particolari per calcolarne il perimetro o l'area. Entrambe le formule fanno uso di pi o π.

Partendo da questo, possiamo trovare la formula della circonferenza di un cerchio (il suo perimetro):

Dove $d$ è il diametro. Questo è il modo in cui $\pi$ viene più spesso definito: invertendo la formula, lo troverai come rapporto tra il perimetro di un cerchio e il suo diametro.

In termini di pizza, questa è la lunghezza della crosta (del bordo esterno). Per ora non ci interessa questa quantità, perché la bontà della pizza si trova all'interno della crosta! Per calcolare questa quantità, dobbiamo imparare a calcolare l'area di un cerchio.

Per farlo, utilizziamo la seguente formula:

La prima cosa che notiamo è che non usiamo più il diametro, ma il raggio. Puoi vedere il perché nella seguente illustrazione.

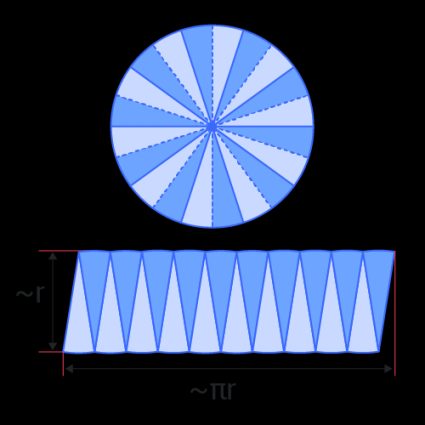
Indipendentemente dall'illustrazione, puoi già notare una differenza fondamentale nella formula: la lunghezza (il diametro nella circonferenza e il raggio nell'area) scala con un esponente diverso.

Quali sono le conseguenze di un esponente diverso nel calcolo del perimetro e dell'area? Anche se non è semplice confrontare una lunghezza (la circonferenza) e un'area, possiamo vedere come i comportamenti differiscono utilizzando un semplice confronto.

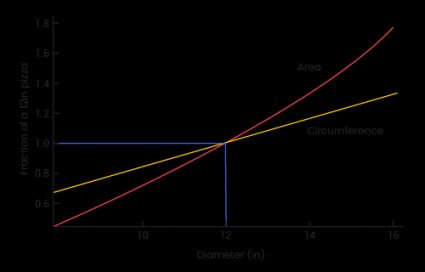
Questo grafico mostra la crescita della circonferenza e dell'area di una pizza in funzione del diametro crescente. Per permetterti di confrontare una lunghezza (il diametro, in cm) e un'area (in cm²), abbiamo scalato queste quantità usando come riferimento una pizza media da 30 centimetri o equivalente a 12 pollici. Questo ci permette di identificare tre regioni del grafico:

• Per un diametro di 30 centimetri, la circonferenza e l'area della pizza corrispondono al riferimento. Ci troviamo quindi all'intersezione della curva.

• Per diametri più piccoli di 30 centimetri, la circonferenza è più grande dell'area se la confrontiamo con il riferimento. Questo significa che per una pizza più piccola di 30 centimetri, avrai relativamente più crosta che condimenti!

• Per diametri superiori a 30 centimetri, la area inizia a crescere molto più velocemente della circonferenza. Rispetto al riferimento, le pizze più grandi hanno molto più ripieno di quelle più piccole.

Vale la pena di dire che optare per una pizza più grande è quasi sempre più conveniente. Come in qualsiasi altro settore, le pizzerie hanno margini di guadagno migliori sui prodotti più piccoli. La tabella seguente mostra come l'area di una pizza cresca rapidamente all'aumentare del diametro. Di conseguenza, una pizza da 18 pollici è tre volte più grande di una da 10 pollici. Allo stesso tempo, una pizza gigante da 61 cm sfamerà più persone di due da 40 cm o di quasi sei da 25 cm.

Assicurati di utilizzare il nostro calcolatore la prossima volta che ordini delle pizze con gli amici. Sarete grati di aver fatto i conti quando arriverà i vostri ordini. Ora non sono solo gli sconti a farvi risparmiare!

Il calcolatore per il confronto delle pizze richiede uno sforzo minimo da parte tua. Basta inserire il diametro, il prezzo e il numero di pizze più piccole e ripetere l'operazione per la pizza o le pizze più grandi che stai considerando. Questo strumento ti mostrerà le aree delle pizze e il costo totale, e poi confronterà il tutto e ti comunicherà il risparmio in percentuale. Se vuoi confrontare solo le aree e non i prezzi, questo strumento funziona in entrambi i casi. Le unità di misura saranno quelle predefinite del tuo paese, ma sei libero di passare dal sistema metrico a quello imperiale a tuo piacimento, o magari di prendere 3000 millimetri di pizza!