Calculateur de combinaison

Ce calculateur de combinaison – calculateur « k parmi n » – est un outil qui vous aide non seulement à déterminer le nombre de combinaisons dans un ensemble, mais vous montre aussi chaque combinaison (ou permutation) possible de votre ensemble. Il est capable de gérer des ensembles de tailles allant jusqu'à 20 éléments. Attention ! Générer des combinaisons de grande taille peut prendre quelques secondes. Si vous vous demandez combien de combinaisons différentes peuvent être obtenues à partir d'un nombre d'éléments et d'une taille d'échantillon donnés, essayez notre calculateur de combinaison dès maintenant !

Vous ne savez toujours pas ce qu'est une combinaison ? Ne vous inquiétez pas, cet article est là pour vous expliquer. Vous trouverez ici une définition de la combinaison, la formule de la combinaison (avec et sans répétitions) et la manière de calculer les combinaisons. Vous apprendrez également tout ce qu'il faut savoir sur les combinaisons linéaires et les probabilités dites combinatoires. Enfin, nous vous parlerons de la relation entre la permutation et la combinaison. En bref, la permutation tient compte de l'ordre des éléments, ce qui n'est pas le cas de la combinaison. Poursuivez votre lecture pour en savoir plus !

Vous vous êtes sûrement déjà demandé·e quelles étaient vos chances de gagner le premier prix d'une loterie ? Ou même quelle était la probabilité de gagner le deuxième prix ? Pour répondre à ces deux questions et bien d'autres encore, vous devez utiliser des combinaisons. Nous disposons d'un outil spécialement dédié à ce type de problème. Notre calculateur de loterie 🇺🇸 ne se contente pas d'estimer la probabilité de combinaison pour gagner à un jeu de loterie, mais fournit également une formule de loterie. Essayez-le ! Vous découvrirez à quel point ces chiffres sont grands (ou petits, d'ailleurs).

Une combinaison est le nombre de façons dont vous pouvez choisir k éléments dans un ensemble contenant n objets distincts (c'est pourquoi ces problèmes sont souvent appelés problèmes « k parmi n »). L'ordre dans lequel vous choisissez les éléments n'est pas important contrairement à une permutation. Pour plus d'informations sur la différence entre une combinaison et une permutation, consultez la section Permutation et combinaison.

La recherche de toutes les combinaisons d'un ensemble d'objets est un problème purement mathématique. On vous a probablement déjà appris, par exemple, à trouver le plus grand commun diviseur (PGCD) ou le plus petit commun multiple (PPCM). Une combinaison est une tout autre histoire. Voyons pourquoi !

Imaginez un sac rempli de douze boules, chacune d'une couleur différente. Vous prenez cinq boules au hasard. Combien d'ensembles distincts de boules pouvez-vous obtenir ? Ou, en d'autres termes, combien de combinaisons différentes pouvez-vous obtenir ?

Les mathématiciens ont trouvé des formules exactes pour calculer de nombreux types de mesures, comme la surface et le volume. Est-il possible d'appliquer une approche similaire pour estimer le nombre de combinaisons possibles avec des boules ?

La bonne nouvelle, c'est que vous n'avez pas besoin de lister tous les ensembles possibles. Mais alors, comment calculer les combinaisons ? En utilisant la formule suivante, vous pouvez déterminer le nombre de combinaisons en un rien de temps :

où :

• $C_{n}^{k}$ – le nombre de combinaisons
• $n$ – le nombre total d'éléments dans l'ensemble
• $k$ – le nombre d'éléments que vous choisissez dans cet ensemble

Le point d'exclamation $!$ représente une factorielle. Consultez notre calculateur de factorielle 🇺🇸 pour plus d'informations sur ce sujet. L'expression du côté droit est également connue sous le nom de coefficient binomial.

Appliquons cette équation à notre problème de boules colorées. Nous devons déterminer le nombre de combinaisons possibles :

Vous pouvez vérifier le résultat avec notre calculateur « k parmi n ». Il vous fournira également une liste de toutes les combinaisons possibles ! Sachez toutefois que 792 combinaisons différentes, c'est déjà beaucoup. Pour éviter qu'il y ait trop de combinaisons générées, nous avons limité ce générateur de combinaisons à un nombre maximum de combinaisons (2 000 par défaut). Vous pouvez modifier ce nombre dans le Mode avancé (Advanced mode) quand vous le souhaitez.

Notez que la formule de combinaison indique que le nombre de combinaisons pour choisir un seul élément est égal au nombre total d'éléments $n$. En revanche, si vous devez choisir tous les éléments, il n'y a qu'une seule combinaison possible.

Voyons comment cela fonctionne avec notre exemple. Nous avons un ensemble de $n = 12$ boules, chacune d'une couleur différente. Dans notre calculateur « k parmi n », les couleurs sont représentées par des lettres, par exemple, A pour rouge, B pour jaune, C pour vert, etc. Si nous choisissons un seul élément $k = 1$ à la fois, il y a $12$ combinaisons possibles, car il y a 12 boules différentes. En revanche, si nous choisissons $k = 12$ éléments, il n'y a que $1$ combinaisons possibles, puisqu'il n'y a qu'une seule façon de choisir toutes les boules.

Essayez vous-même avec notre calculateur de combinaison !

À ce stade, vous avez probablement une bonne compréhension des combinaisons et de la formule de combinaison. Si vous souhaitez en savoir plus, les sections suivantes couvriront les différences entre les combinaisons et les permutations (qui sont souvent considérées à tort comme la même chose), la probabilité combinatoire et la combinaison linéaire.

Imaginez que vous ayez le même sac rempli de boules colorées que dans l'exemple de la section précédente. Vous choisissez à nouveau cinq boules au hasard, mais cette fois, l'ordre est important – il importe que vous choisissiez la boule rouge en premier ou en troisième. Dans un premier temps, prenons un exemple plus simple dans lequel vous choisissez trois boules appelées R (rouge), B (bleu), V (vert). Il existe six permutations possibles de cet ensemble (l'ordre des lettres détermine l'ordre des boules sélectionnées) : RBV, RVB, BRV, BVR, VRB, VBR. Mais, selon la définition de la combinaison, il n'y a qu'une seule combinaison ! C'est la différence fondamentale entre les combinaisons et les permutations.

Par définition, une permutation est une réorganisation de tous les éléments d'un ensemble dans un certain ordre. Dans la littérature, on considère que toutes les permutations sont possibles, même celles qui ne contiennent pas tous les éléments de l'ensemble. C'est ce qui rend la permutation et la combinaison similaires. La permutation peut alors désigner une réorganisation de k éléments d'un ensemble de n objets distincts. Si vous souhaitez une explication plus approfondie, le calculateur de permutation 🇺🇸 devrait vous satisfaire.

La formule de permutation est la suivante :

Cette équation ne ressemble-t-elle pas à la formule de combinaison ? En effet, si vous connaissez le nombre de combinaisons, vous pouvez facilement calculer le nombre de permutations :

Si vous activez le Mode avancé (Advanced mode) de ce calculateur de combinaison, vous pourrez trouver le nombre de permutations.

Vous vous demandez peut-être pourquoi utiliser une permutation au lieu d'une combinaison. La première question à se poser est de savoir si l'ordre est important ou non ? Par exemple, supposons que vous disposiez d'un jeu de neuf cartes avec des chiffres de 1 à 9. Vous tirez trois cartes au hasard et les alignez sur la table, créant ainsi un nombre à trois chiffres, par exemple 425 ou 837. Combien de nombres distincts pouvez-vous former ?

Vérifiez le résultat avec notre Calculateur Omni ! Et combien y a-t-il de combinaisons différentes ?

Le nombre de combinaisons est toujours inférieur au nombre de permutations. Cette fois, il est six fois plus petit (si vous multipliez 84 par $3! = 6$, vous obtiendrez 504). Cela s'explique par le fait que les trois cartes que vous choisissez peuvent être réarrangées de six façons différentes, comme dans l'exemple précédent avec les boules de trois couleurs.

Pour compléter notre discussion sur les permutations et les combinaisons, nous devons introduire une nouvelle notion, celle de sélection avec répétitions autorisées. Cela signifie qu'à chaque fois que vous choisissez un élément de l'ensemble de n objets distincts, vous le remettez dans cet ensemble. Dans l'exemple des boules colorées, vous prenez une boule dans le sac, vous la mémorisez et, vous la remettez dans le sac. De la même manière, dans le deuxième exemple avec les cartes, vous sélectionnez une carte, vous notez le numéro de cette carte et vous la remettez dans le jeu. De cette façon, vous pouvez avoir, par exemple, deux boules rouges dans votre combinaison ou 228 comme permutation.

Vous imaginez peut-être que ces formules sont compliquées. En réalité, elles ne sont pas aussi complexes que vous le pensez. Par exemple, calculer la teneur en alcool de votre bière artisanale est plus difficile. Dans le cas des permutations, l'équation est encore plus simple. La formule de combinaison avec répétition est la suivante :

et pour la permutation avec répétition :

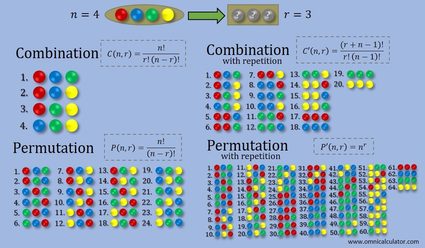
L'image ci-dessous présente un résumé des différences entre les quatre types de sélection d'objets : combinaison, combinaison avec répétition, permutation et permutation avec répétition. Dans cet exemple, nous avons quatre boules de différentes couleurs et nous en choisissons trois. Dans le cas des sélections avec répétition, nous pouvons choisir une même boule plusieurs fois. Si vous voulez essayer avec les permutations, sachez que cela peut donner lieu à des milliers de résultats différents ! Néanmoins, vous pouvez toujours calculer le nombre de résultats possibles avec notre calculateur (les permutations se trouvent dans le Mode avancé (Advanced mode))

Commençons par la probabilité combinatoire, essentielle dans de nombreux problèmes statistiques. Un exemple illustré juste au-dessus devrait l'expliquer facilement : vous choisissez trois boules colorées sur quatre dans le sac. Supposons que vous souhaitiez connaître les chances (probabilités) qu'il y ait une boule rouge parmi elles. Il existe quatre combinaisons différentes, et la boule rouge se trouve dans trois d'entre elles. La probabilité de la combinaison est donc la suivante :

Si vous tirez trois boules au hasard dans le sac, dans 75 % des cas, vous choisirez une boule rouge. Pour exprimer une probabilité, on utilise généralement le signe du pourcentage.

Supposons maintenant que vous choisissiez une boule, que vous notiez la couleur obtenue et que vous la remettiez dans le sac. Quelle est la probabilité combinatoire que vous obteniez au moins une boule rouge ? Il s'agit d'un problème de « combinaison avec répétition ». Dans l'image ci-dessus, vous pouvez voir qu'il y a vingt combinaisons au total et que la boule rouge se trouve dans dix d'entre elles :

Est-ce une surprise pour vous ? Eh bien, cela ne devrait pas l'être. Lorsque vous remettez la première boule, par exemple la boule bleue, vous pouvez également la tirer comme deuxième et troisième boule. Les chances d'obtenir une boule rouge sont donc réduites. Vous pouvez faire des considérations analogues avec la permutation. Essayez de résoudre un problème avec ce même sac de boules colorées : quelle est la probabilité que votre première boule tirée soit rouge ?

Supposons que vous ne nous fassiez pas confiance et que vous souhaitiez essayer de le faire vous-même. Vous tirez trois boules sur quatre et vous vérifiez s'il y a une boule rouge ou non (comme dans le premier exemple de cette section). Vous répétez ce processus trois fois de plus, et vous n'obtenez la boule rouge que dans un cas sur quatre, soit $25 \ \%$ des cas. Vous vous attendiez à $75\ \%$ selon la théorie. Alors que s'est-il passé ? Eh bien, c'est ainsi que fonctionnent les probabilités ! La loi des grands nombres décrit le résultat de la réalisation d'une même expérience un grand nombre de fois. Si vous répétez le tirage, par exemple cent fois, vous serez beaucoup plus proche de $75\ \%$.

De plus, la loi des grands nombres conduit presque toujours à la loi normale centrée réduite (ou loi normale standard), qui peut décrire, par exemple, l'intelligence ou la taille des personnes, avec ce que l'on appelle la valeur p. Vous voulez en savoir plus ? Le calculateur de loi normale 🇺🇸 est l'outil qu'il vous faut !

Avez-vous déjà entendu parler de la combinaison linéaire ? En fait, bien qu'elle contienne le mot combinaison, elle n'a pas grand-chose à voir avec ce que nous avons appris jusqu'à présent. Néanmoins, nous allons essayer de l'expliquer brièvement. Une combinaison linéaire est le résultat d'un ensemble de termes multiplié par une constante et additionné. Elle est fréquemment utilisée en physique des ondes pour prédire l'équation du réseau de diffraction ou même en physique quantique à cause de l'équation de de Broglie. Voici quelques exemples courants de combinaison linéaire :

1. Vecteurs. Chaque vecteur à 3 dimensions peut être décomposé en trois vecteurs unitaires $\^e_1 = (1,0,0)$, $\^e_2 = (0,1,0)$ et $\^e_3 = (0,0,1)$. Par exemple, $\vec{v} = (2,5,3) = 2\^e_1 + 5\^e_2 + 3\^e_3$ et c'est une combinaison linéaire.
2. Fonctions. Supposons que vous ayez deux fonctions $f(x) = \text{e}^x$ et $g(x) = \text{e}^{-x}$. À partir de ces deux fonctions, vous pouvez créer des combinaisons linéaires qui décrivent le sinus hyperbolique : $\sinh(x) = \frac{f(x)}{2} - \frac{g(x)}{2}$ ou le cosinus : $\cosh(x) = \frac{f(x)}{2} + \frac{g(x)}{2}.$ Vous pouvez faire la même chose avec le sinus et le cosinus normaux, mais vous devez utiliser le nombre imaginaire $i$. Nous en parlons plus en détail dans la dernière section du calculateur de racine carrée 🇺🇸.
3. Polynômes. Par exemple, vous avez trois polynômes $p_1(x) = 1$, $p_2(x) = 3x + 3$, $p_3(x) = x^2 -x + 1$ et vous voulez exprimer la fonction $q(x) = 2x^2 + x + 3$ comme une combinaison linéaire de ces polynômes. Ce n'est pas toujours possible, mais dans ce cas $q(x) = -2p_1(x) + p_2(x) + 2p_3(x).$

La différence fondamentale entre la combinaison et la permutation en mathématiques réside dans le fait que l'on se préoccupe ou non de l'ordre des éléments.

• Dans la permutation, l'ordre est important, nous disposons donc les éléments dans un ordre séquentiel.
• Dans la combinaison, l'ordre n'a pas d'importance, nous sélectionnons alors un groupe d'éléments dans une collection plus large.

Si vous avez déjà une combinaison et que vous voulez la transformer en permutation, vous devez imposer un ordre à l'ensemble des éléments, c'est-à-dire choisir l'un des ordres possibles pour votre ensemble. Ainsi, le nombre de permutations de k éléments choisis parmi n éléments est égal au nombre de combinaisons de k éléments choisis parmi n éléments multiplié par le nombre d'arrangements de ces k éléments, à savoir par k!.

Si vous avez déjà une permutation et que vous voulez la transformer en combinaison, vous devez supprimer l'ordre, c'est-à-dire considérer toutes les réorganisations possibles comme le même objet. Par conséquent, le nombre de combinaisons de k éléments choisis parmi n éléments est égal au nombre de permutations de k éléments choisis parmi n éléments divisé par le nombre d'arrangements de ces k éléments, à savoir par k!.

Si le mot comporte sept lettres distinctes, vous avez 7! = 5 040 façons de les arranger (permutations simples de sept éléments). Cependant, si certaines lettres apparaissent plus d'une fois, le nombre d'arrangements diminue ! Par exemple :

• si le mot est « POMME », « M » apparaît deux fois, nous divisons donc 5! par 2! = 2 et le résultat est 60 ;
• si le mot est « BANANE », nous avons « N » et « A » qui apparaissent deux fois, donc nous divisons 6! par 2! × 2!= 4 et le résultat est 180 ;
• si le mot est « CASSIS », nous avons « S » trois fois, donc nous divisons 6! par 3! = 6 et le résultat est 120.