Calculateur de suite géométrique

Calculez tout ce que vous voulez sur les suites géométriques avec notre calculateur de suite géométrique. Ce calculateur vous aidera à comprendre la définition, les formules et les applications des suites géométriques.

Nous expliquons la différence entre les deux équations de suites géométriques, la formule explicite et la formule par récurrence. Nous vous montrons également comment utiliser ces formules pour résoudre des problèmes intéressants.

Nous avons aussi incorporé une fonctionnalité de calculateur de séries géométriques qui évalue la somme d'une suite géométrique. Cette fonctionnalité utilise la formule explicite de la suite géométrique pour arriver à la formule de la série géométrique.

Une suite géométrique est une collection de nombres, dans laquelle tous les nombres, sauf le premier, sont obtenus en multipliant le précédent par un nombre fixe, non nul, appelé la raison. Si vous avez du mal à comprendre ce qu'est une suite géométrique, ne vous inquiétez pas ! Nous expliquerons plus loin ce que cela signifie en termes plus simples et nous examinerons les formules par récurrence et explicite d'une suite géométrique. Nous inclurons également quelques exemples de suites géométriques.

Avant de s'attarder plus en détails sur la définition, il est important de clarifier certains points pour éviter toute confusion. Tout d'abord, nous devons comprendre que la suite géométrique n'a rien à voir avec la factorielle. Même si une suite géométrique se crée en multipliant constamment des nombres par un facteur, cela n'a aucun lien avec l'opération factorielle, qui est le produit de tous les entiers positifs inférieurs ou égaux à un certain nombre. Le plus grand commun diviseur (PGCD) et le plus petit commun multiple (PPCM) sont liés aux suites géométriques, mais pas de la manière dont vous pourriez le penser. Si le premier nombre d'une suite géométrique est un entier, alors tous les nombres de la suite partagent le même PGCD ou PPCM.

Cela signifie que le PGCD (voir le calculateur PGCD) est simplement le plus petit nombre de la suite, et le PPCM, le plus grand nombre. Par exemple, dans la suite 3, 6, 12, 24, 48, le PGCD est 3, et le PPCM serait 48. Mais si nous ne considérons que les nombres 6, 12, 24, le PGCD sera 6 et le PPCM sera 24.

En termes simples, une suite géométrique est une suite de nombres dans laquelle chacun nombre est obtenu en multipliant le précédent par un nombre fixe, appelé la raison, que nous avons mentionnée précédemment. La raison est l'une des deux caractéristiques déterminantes d'une suite géométrique, l'autre étant le premier terme. Nous verrons plus tard comment ces deux nombres sont utilisés pour définir une suite géométrique et pour obtenir les formules par récurrence et explicite.

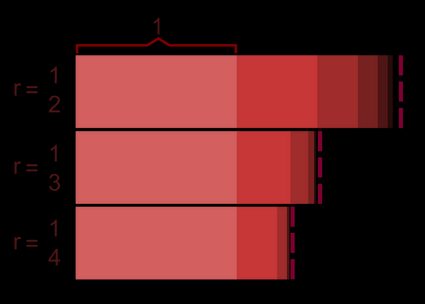
Construisons maintenant une suite géométrique simple en utilisant des valeurs concrètes pour ces deux paramètres déterminants. Pour simplifier les choses, nous prendrons le premier terme égal à $1$, et la raison égale à $2$. Dans ce cas, le premier terme sera par définition $u_1 = 1$, le deuxième terme sera $u_2 = u_1 × 2 = 2$, le troisième terme sera alors $u_3 = u_1 × 2^2 = u_2 × 2 = 4$, etc. Le n-ième terme de la suite serait ainsi :

où $n$ est la position du terme en question dans la suite.

On constate que le rapport de deux termes consécutifs quelconques de la suite (comme il est défini dans notre calculateur de ratio) est constant et égal à la raison.

Une façon courante d'écrire une suite géométrique est d'écrire explicitement les premiers termes. Cela vous permet de calculer n'importe quel autre nombre de la suite. Pour notre exemple, nous écririons la suite de la façon suivante :

On peut également utiliser des formules mathématiques pour décrire une suite géométrique. Ces formules sont appelées formules explicite et par récurrence. Maintenant que nous savons ce qu'est une suite géométrique, nous pouvons en apprendre davantage sur ces formules et découvrir comment elles donnent les mêmes informations en moins de mots et avec plus de précision.

Il existe deux façons distinctes de représenter mathématiquement une suite géométrique : la formule explicite et la formule par récurrence. La première est celle utilisée dans l'exemple précédent. Nous avons donc vu l'application de cette formule à un exemple particulier, mais il existe une formule générale valable pour toutes les suites géométriques. Pour cela, vous devez remplacer les valeurs de $u_1$ par le premier terme correspondant et $q$ par la raison. La formule générale pour le n-ième terme est la suivante :

où $n \in \mathbb N$ signifie que $n = 1, 2, 3,…$. La formule explicite comporte les informations les plus importantes d'une suite géométrique : le premier terme $u_1$, la manière d'obtenir n'importe quel terme à partir du premier, et le fait qu'il n'y a pas de terme avant ce premier terme.

Il existe un autre type de formule : celle par récurrence. Elle est composée de deux parties, qui comportent d'autres informations que la définition de la suite géométrique. La première partie explique comment passer de n'importe quel terme de la suite à n'importe quel autre terme en utilisant la raison. Cette signification seule n'est pas encore suffisante pour construire une suite géométrique puisque nous ne connaissons pas le point de départ. Nous avons besoin de la deuxième partie de la formule : le premier terme (ou tout autre terme d'ailleurs). Voyons à quoi ressemble cette formule par récurrence :

où $x$ est utilisé pour exprimer le fait que n'importe quel nombre sera utilisé à sa place, mais aussi qu'il doit s'agir d'un nombre explicite et non d'une formule. L'indice $k$ indique n'importe quel nombre naturel (tout comme $n$), mais il est utilisé à la place de $n$ pour préciser que $k$ n'a pas besoin d'être le même nombre que $n$.

Maintenant que vous savez ce qu'est une suite géométrique et comment en construire une avec les formules par récurrence et explicite, il est temps d'appliquer vos connaissances et de calculer quelques petites choses ! Avec notre outil, vous pouvez calculer toutes les propriétés des suites géométriques, telles que la raison, le premier terme, le n-ième dernier terme, etc. Voici une brève description de la structure du calculateur :

1. Tout d'abord, dites-nous ce que vous savez de votre suite en choisissant le modèle :
   • la raison et le premier terme de la suite ;
   • la raison et un n-ième terme ; ou
   • deux termes quelconques.
2. Saisissez vos données. En fonction de ces données, le calculeur détermine l'ensemble de votre suite géométrique.
3. Par défaut, le calculateur affiche les cinq premiers termes de votre suite. Vous pouvez modifier les premiers et derniers termes en fonction de vos besoins.

Notre outil peut également calculer la somme de votre suite : en totalité ou en partie. Dans ce dernier cas, il suffit de saisir le point de départ et le point final de la somme, et vous pouvez profiter du résultat. Comme vous l'apprendrez dans les sections suivantes, la somme infinie n'existe peut-être pas !

Jusqu'à présent, nous avons parlé de suites géométriques comme des collections de nombres. Cependant, il peut aussi être intéressant d'essayer d'additionner les termes d'une suite géométrique. Dans le cas d'une suite géométrique finie, c'est-à-dire quand le nombre de termes est limité, le processus est aussi simple que de trouver la somme d'une suite de nombres linéaires. Le calcul de la somme de cette suite géométrique peut même être fait à la main, en théorie.

Mais nous pouvons être plus efficaces que cela en utilisant la formule de la série géométrique. Pour ce faire, nous utiliserons le signe mathématique de la sommation $\Sigma$, ce qui signifie qu'il faut additionner tous les termes qui suivent. Par exemple, si nous avons une suite géométrique nommée u_n et que nous nommons la somme de la suite géométrique S, la relation entre les deux serait :

si nous voulons additionner les n premiers termes, ou :

si l'on veut faire la somme de tous les termes.

Il reste à résoudre le problème du calcul de la valeur de la série géométrique. Vous pouvez toujours utiliser ce calculateur comme calculateur de séries géométriques, mais il serait préférable, que vous compreniez comment le faire à la main. Il existe une astuce qui peut vous faciliter la tâche et qui consiste à modifier et à résoudre l'équation de la suite géométrique comme suit :

Multipliez maintenant les deux côtés par $(1-q)$ et résolvez le problème :

Ce résultat, que vous pouvez facilement calculer par vous-même, représente la formule de base de la série géométrique lorsque le nombre de termes de la série est fini. Cependant, il s'agit de mathématiques et non de la vraie vie. Nous pouvons donc avoir un nombre infini de termes dans notre série géométrique et être en mesure de calculer la somme totale de tous les termes. « Comment cela fonctionne-t-il ? » me direz-vous. Eh bien, n'ayez crainte, nous allons tout vous expliquer en détail.

Après avoir vu comment obtenir la formule de la série géométrique pour un nombre fini de termes, il est naturel (du moins pour les mathématiciens) de se demander comment on calcule la somme infinie d'une suite géométrique ? Cela peut sembler impossible, mais certaines astuces permettent de calculer cette valeur en seulement quelques étapes. Pour cela, nous devons introduire le concept de limite. Il s'agit d'un procédé mathématique par lequel on peut comprendre ce qui se passe du côté de l'infini. Il peut également être utilisé pour tenter de définir mathématiquement des expressions qui sont habituellement indéfinies, comme zéro divisé par zéro ou zéro à la puissance zéro.

Parler des limites est un sujet très complexe, qui dépasse le cadre de ce calculateur. Leur complexité est la raison pour laquelle nous avons décidé de les mentionner, mais de ne pas entrer trop en détails concernant la façon de les calculer. Ne vous inquiétez pas : vous trouverez d'excellentes informations dans l'article de Wikipédia sur les limites.

Même si vous n'avez pas envie d'en savoir plus sur les limites en général, vous pouvez toujours calculer la somme infinie d'une série géométrique à l'aide de notre calculateur. Il est important de noter que toutes les séries n'ont pas une somme définie. Les conditions qu'une série doit remplir pour que sa somme soit un nombre (ce que les mathématiciens appellent la convergence) sont, en principe, simples. Nous les expliquons dans la section suivante.

Les séries mathématiques (à la fois pour les suites géométriques et arithmétiques) sont souvent divisées en deux catégories : les séries convergentes, dont la somme infinie est finie, et les séries divergentes, dont la somme infinie est infinie ou non définie. La meilleure façon de savoir si une série est convergente ou non est de calculer sa somme infinie à l'aide de limites. Toutefois, il existe quelques astuces qui permettent de distinguer rapidement les séries convergentes des séries divergentes sans avoir à faire tous ces calculs. Parmi ces astuces, on peut citer : regarder le terme initial et le terme général, regarder le rapport entre les termes successifs, ou encore comparer ces séries avec d'autres séries similaires.

Pour qu'une série soit convergente, le terme général $u_n$ doit devenir de plus en plus petit à chaque augmentation de la valeur de $n$. Si $u_n$ devient de plus en plus petit, nous ne pouvons pas garantir que la série sera convergente, mais si $u_n$ est constant ou devient de plus en plus grand lorsque $n$ augmente, nous pouvons affirmer que la série sera divergente. Si nous ne sommes pas sûrs que $u_n$ diminue, nous pouvons examiner le premier terme et la raison ou même calculer certains des premiers termes. Cela nous donnera une idée de la façon dont $u_n$ évolue.

La deuxième option consiste à comparer l'évolution de notre série géométrique à une série dont nous sommes certains qu'elle converge (ou diverge), ce qui peut être fait en effectuant une recherche rapide en ligne. D'une manière générale, si la série que nous étudions est plus petite (c'est-à-dire que $u_n$ est plus petit) qu'une série dont nous savons avec certitude qu'elle converge, nous pouvons être sûrs que notre série convergera également. Inversement, si notre série est plus grande qu'une série dont nous sommes sûrs qu'elle est divergente, notre série divergera toujours. Dans les autres cas, la convergence de notre série géométrique est incertaine, à savoir lorsque que notre terme $u_n$ est plus grand qu'une série qui converge ou lorsque qu'il est plus petit qu'une série qui diverge. Il est nécessaire de trouver une autre série à laquelle la comparer ou d'utiliser une autre méthode pour déterminer la convergence de la série.

Ces critères s'appliquent aux séries arithmétiques et géométriques. En fait, ces deux séries sont étroitement liées l'une à l'autre et les deux suites peuvent être reliées par les opérations d'exponentiation et de calcul des logarithmes.

Nous avons déjà vu un exemple de suite géométrique avec la suite des puissances de deux. Il s'agit d'une suite très importante en raison des ordinateurs et de leur représentation binaire des données. À travers cette suite, nous pouvons trouver des valeurs telles que le nombre maximum autorisé dans un ordinateur (varie en fonction du type de variable utilisé), le nombre d'octets dans un gigaoctet, ou le nombre de secondes jusqu'à la fin de l'heure UNIX (à la fois les valeurs originales et intercalaires).

En plus de la suite des puissances de deux, nous pouvons obtenir n'importe quelle autre suite de puissances en remplaçant simplement $q = 2$ par la valeur de la base qui nous intéresse. Les séries de puissances sont couramment utilisées et largement connues, et peuvent être exprimées à l'aide de la formule des suites géométriques. Nous vous montrerons des séries géométriques encore plus importantes ou intéressantes, comme les séries alternées ou l'époustouflant paradoxe de Zénon.

Commençons par les paradoxes de Zénon, aussi appelé le paradoxe de la dichotomie. Ce paradoxe n'est au fond qu'une énigme mathématique sous la forme d'une série géométrique infinie. Zénon était un philosophe grec antérieur à Socrate. Il a conçu un mécanisme qui lui permet de prouver qu'un mouvement est impossible et qu'il ne devrait jamais se produire dans la vie réelle. L'idée est de diviser en deux la distance entre le point de départ (A) et le point d'arrivée (B). Une fois que vous avez parcouru la première moitié, vous divisez à nouveau la distance restante par deux… Vous pouvez répéter ce processus autant de fois que vous le souhaitez, ce qui signifie qu'il vous restera toujours une certaine distance à parcourir pour atteindre le point B.

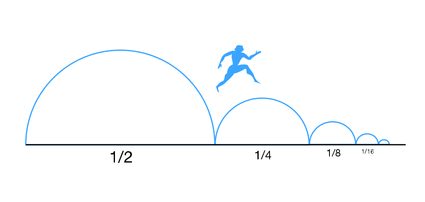
Le paradoxe de Zénon semble prédire que, puisque nous avons un nombre infini de moitiés à parcourir, nous aurions besoin d'un temps infini pour nous rendre d'un point A à un point B. Cependant, comme nous le savons par notre expérience quotidienne, ce n'est pas vrai, et nous pouvons toujours aller d'un point A à un point B en un temps fini (à l'exception des Espagnols qui semblent toujours arriver infiniment en retard partout). La solution à ce paradoxe apparent peut être trouvée en utilisant les mathématiques.

Si nous exprimons le temps nécessaire pour aller de A à B (appelons-le $t$ pour l'instant) sous la forme d'une série géométrique, nous aurons une série définie par : $u_1 = t/2$ avec pour raison $q = 1/2$. Il faudrait donc parcourir la première moitié du trajet en $t/2$, puis couvrir la moitié de la distance restante en $t/4$, puis $t/8$, etc. Si nous écrivons maintenant la somme infinie de la série géométrique, nous trouverons que :

Il s'agit de la preuve mathématique que l'on peut aller de A à B en un temps fini ($t$ dans ce cas).

Pour terminer, et au cas où le paradoxe de Zénon n'aurait pas suffi à vous époustoufler, mentionnons les séries alternées.

Cette série commence à $u_1 = 1$ et a une raison $q = -1$ qui donne une série de la forme :

Cette série ne converge pas selon les critères habituels, car le résultat dépend du nombre pair ($S = 0$) ou impair ($S = 1$) de termes. Il existe cependant une astuce qui permet de « faire » converger cette série vers un nombre fini. L'astuce en elle-même est très simple, mais elle repose sur des arguments mathématiques (et même méta-mathématiques) très complexes. Par conséquent, si vous montrez cette astuce à un mathématicien, vous risquez d'avoir de gros ennuis (vous obtiendriez une réaction similaire en parlant de la tristement célèbre conjecture de Syracuse). Vous êtes prévenu·e. Voyons maintenant cette soi-disant « solution » :

Nous multiplions les deux côtés par $-1$ :

Si nous résolvons $S$ maintenant :

Vous pouvez maintenant aller frimer auprès de vos amis, à condition qu'ils ne soient pas mathématiciens.

Une suite géométrique est une collection de nombres telle que le terme suivant est obtenu en multipliant le terme précédent par un nombre commun.

Pour trouver la somme d'une suite géométrique :

1. Calculez la raison, q élevée à la puissance n.
2. Soustrayez le résultat qⁿ de 1.
3. Divisez le résultat par (1 - q).
4. Multipliez la résultante par le premier terme, u₁.

Pour trouver le n-ième terme d'une suite géométrique :

1. Calculez la raison élevée à la puissance (n-1).
2. Multipliez le résultat par le premier terme, u₁.

Pour calculer la raison d'une suite géométrique, divisez deux termes consécutifs quelconques de la suite.