Calculateur de comparaison de pizzas (Ancienne version)

Consultez le calculateur de taille de pizza 🇺🇸, notre nouvelle version du calculateur de comparaison de pizzas 🍕

Combien de fois vous êtes-vous demandé·e s'il valait mieux prendre 2 pizzas de tailles moyennes ou 1 grande pizza ? Ou fini par taper « comparaison de pizzas » sur internet dans l'espoir de faire le bon choix pour satisfaire vos envies ? Il est probable que vous soyez nombreux et nombreuses à vous poser ces questions. Les pizzerias vous indiquent généralement le diamètre de la pizza, mais nous ne mangeons pas le diamètre. Nous ne mangeons pas non plus la circonférence. Ce que nous mangeons, c'est l'aire de la pizza. Il s'agit d'un calcul très simple qui tourne autour de l'équation : aire = rayon² × π. Mais nous sommes souvent trop pressés ou ne pouvons tout simplement pas nous donner la peine de le calculer de tête. C'est pourquoi nous avons conçu ce calculateur de comparaison de pizzas pour résoudre ces problèmes une bonne fois pour toutes. Lisez la suite pour découvrir les mathématiques cachées derrière le calculateur de comparaison de pizzas et pour voir comment la circonférence et l'aire d'une pizza augmentent différemment en prenant pour référence une pizza de 30 cm (12 pouces). Dans cet article, vous apprendrez :

• comment effectuer une comparaison mathématiquement correcte des pizzas ;
• pourquoi on utilise une pizza de 30 cm (12 pouces) dans la comparaison des tailles ; et
• comment utiliser notre calculateur de comparaison de pizzas.

Quelle est la géométrie d'une pizza ? Tout réside dans les cercles. Le cercle est une forme basique, sans doute la plus simple ou la plus complexe que vous puissiez imaginer. Composés d'un nombre infini de côtés disposés à une distance constante d'un point central, les cercles exigent certaines formules particulières pour calculer leur circonférence ou leur aire. Ces deux formules utilisent notamment pi, ou π.

En partant de là, on peut trouver la formule de la circonférence d'un cercle (son périmètre) :

Où $d$ est le diamètre. C'est ainsi que $\pi$ est le plus souvent défini : inversez la formule et vous verrez que $\pi$ est le rapport entre la circonférence d'un cercle et son diamètre.

En ce qui concerne les pizzas, la circonférence est la longueur de la croûte (de son bord extérieur). Cette mesure ne nous intéresse pas pour l'instant, car c'est à l'intérieur de la croûte que se trouve tout le plaisir de la pizza ! Pour calculer cette quantité, nous devons apprendre à calculer l'aire d'un cercle.

Pour ce faire, nous utilisons la formule suivante :

La première chose que l'on remarque, c'est que l'on n'utilise plus le diamètre, mais le rayon. Vous pouvez voir pourquoi dans l'illustration suivante.

Quelle que soit l'illustration, vous pouvez déjà constater une différence fondamentale dans les équations : la longueur (le diamètre dans la formule de la circonférence et le rayon dans celle de l'aire) se calcule avec une puissance différente.

Quelles sont les conséquences d'une puissance différente lors du calcul de la circonférence et de l'aire ? Bien qu'il ne soit pas évident de comparer une longueur (la circonférence) et une superficie (l'aire), nous pouvons voir comment les comportements diffèrent en utilisant une simple comparaison.

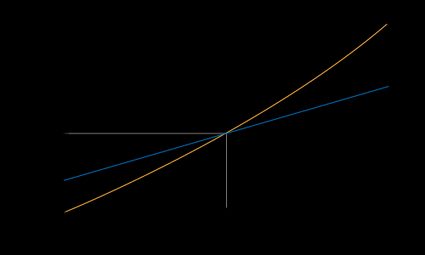
Ce graphique représente la croissance de la circonférence et de l'aire d'une pizza en fonction de l'évolution de son diamètre. Pour vous permettre de comparer une longueur (le diamètre, avec des unités en pouce) et une aire (la superficie, avec des unités en ²), nous avons réduit l'échelle de ces quantités en utilisant comme référence une pizza moyenne de 30 cm (12 pouces). Ainsi, nous pouvons identifier trois régions sur le graphique.

• Pour un diamètre de 30 cm (12 pouces), la circonférence et l'aire de la pizza correspondent à la référence. Nous sommes donc à l'intersection des courbes.

• Pour les diamètres inférieurs à 30 cm (12 pouces), la circonférence est plus grande que l'aire. Cela signifie que pour une pizza de moins de 30 cm (12 pouces), vous obtiendrez relativement plus de croûte que de garniture.

• Pour les diamètres supérieurs à 30 cm (12 pouces), l'aire commence à croître beaucoup plus vite que la circonférence. Par rapport à la référence, les pizzas plus grandes ont beaucoup plus de garniture que les plus petites.

Il convient de préciser qu'il est presque toujours plus rentable d'opter pour une pizza plus grande. Comme dans tout autre branche d'activité, les pizzerias réalisent de meilleures marges sur les produits plus petits. Le tableau ci-dessous montre la rapidité avec laquelle l'aire d'une pizza augmente en fonction de son diamètre. Ainsi, une pizza de 45 cm est plus de trois fois plus grande qu'une pizza de 25 cm. En même temps, une pizza monstrueuse de 61 cm nourrira plus de personnes que deux pizzas de 40 cm ou que près de six pizzas de 25 cm.

Assurez-vous d'utiliser notre calculateur la prochaine fois que vous commanderez une pizza. Vous vous féliciterez d'avoir fait le calcul lorsque votre commande arrivera. Il n'y a pas que les réductions qui peuvent vous faire économiser de l'argent !

Le calculateur de comparaison de pizzas exige un effort vraiment minime de votre part. Il vous suffit de saisir le diamètre, le prix et le nombre des pizzas plus petites et de répéter l'opération pour la ou les pizzas plus grandes que vous envisagez d'acheter. Cet outil vous indiquera l'aire totale et le prix de chaque pizza, ainsi que leur comparaison, exprimée en pourcentage. Si vous souhaitez uniquement comparer les aires, laissez le champ « Prix » vide, notre outil Omni fera le calcul dans les deux cas. Les unités seront par défaut celles de votre pays, mais n'hésitez pas à passer du système métrique au système impérial comme vous le souhaitez, ou peut-être voudriez-vous commander 3 000 millimètres de pizza !