Calculateur Terre plate vs Terre ronde

Quelle est la meilleure façon d'apprendre à connaître le monde ? Est-ce proposer une théorie et la prouver à travers des observations et de la science ? Ou est-ce inventer des choses absurdes et ignorer les faits ? Chez Omni, nous avons tendance à penser que la première option fonctionne plutôt bien. C’est précisément en réfléchissant ainsi que l’on a pu aller sur la Lune, n’est-ce pas ? (Oui, oui! On y est bien allés, d’ailleurs)

Pour célébrer la Journée mondiale de la science au service de la paix et du développement, qui a lieu le 10 novembre de chaque année, nous avons créé un calculateur qui vous aidera à combattre les bêtises, les demi-vérités et les sornettes pour défendre la science, l'observation et l'ouverture d'esprit.

Le calculateur Terre plate vs Terre ronde d'Omni propose des expériences qui prouvent que la Terre est bien ronde. Ne vous inquiétez pas, vous n'aurez pas à construire votre propre fusée pour aller vérifier dans l'espace. Vous ne devrez pas non plus faire des calculs d'impulsion et de quantité de mouvement 🇺🇸 ou d'énergie cinétique.

Nous vous proposons trois expériences relativement simples à réaliser. 

• Ombre d'un bâton : utilisez la longueur des ombres projetées par un bâton à différents endroits pour estimer la circonférence de la Terre.
• Double coucher de soleil : en vous déplaçant, votre perspective change. Par conséquent, il est possible de voir un coucher de soleil deux fois, ou plus précisément, de « prolonger » le coucher de soleil.
• Objets qui disparaissent : cachez des objets derrière la courbure de la Terre en déplaçant votre point de vue vers le bas. Ce calculateur vous indiquera la proportion de l'objet que vous pouvez faire disparaître.

Avant de passer aux expériences, examinons brièvement les raisons qui poussent les gens à croire que la Terre est plate et passons en revue le modèle du monde qu'ils proposent.

Croyez-le ou non, dans le pays le plus riche au monde, et le plus développé du point de vue technologique, 44 % des jeunes âgés de 18 à 24 ans ne sont pas convaincus que la Terre soit ronde 🤔. Bien entendu, il s'agit des États-Unis, et la croyance en une Terre plate peut découler de la culture très individualiste et de la méfiance à l'égard de l'autorité, des institutions et des experts.

Les platistes semblent refuser de voir les preuves des découvertes que l'humanité a rassemblées depuis 2 000 ans. Ils ne savent pas ce qu'ils ratent ! Ils se méfient également de tout ce qu'ils n'ont pas pu vérifier personnellement. Problèmes de confiance ?

Ils se lancent alors dans des défis extraordinaires pour prouver que la Terre est plate, tandis que prouver que la Terre est ronde se révèle beaucoup plus simple. Voici quelques exemples !

• Mad Mike Hughes (Mike le fou) a construit ses propres vaisseaux spatiaux à vapeur pour tenter de voler jusqu'à une hauteur de 1 500 m afin de photographier l'absence de courbure de la Terre. Mais pour ce faire, il faut s'élever à un minimum de 11 000 m. Il est malheureusement décédé en février 2020 à cause de l'échec de l'une de ses fusées.
• La star de YouTube Logan Paul prévoyait de se rendre en Antarctique pour découvrir la limite d'une Terre plate. Cependant, le voyage n'a pas eu lieu en raison de la pandémie de COVID-19 et du manque d'infrastructures médicales pour faire face à l'urgence globale.
• Le rappeur B.o.B a tenté d'utiliser le crowdfunding pour financer le lancement de son propre satellite afin de vérifier si la Terre était plate. Il n'a réussi à récolter que 6 883 dollars du million nécessaire pour réaliser le projet. Tant pis, ce n'est pas grave. Il peut essayer nos expériences simples et peu coûteuses, pas besoin de bouger !

Cette bande dessinée de Tom Fonder illustre assez bien les croyances des platistes.

Dans le modèle de la Terre plate, le monde est un disque, un peu comme un engrenage utilisé pour réduire la vitesse d'une voiture. Le pôle Nord est au centre, alors que la glace et la neige du « pôle Sud » sont situées sur les bords du disque. Donc, le pôle devient une barrière de glace qui empêche l'eau des océans de tomber dans l'espace.

L'épaisseur du disque de la Terre plate n'est pas claire. Cependant, la masse impliquée doit être bien inférieure à celle d'une Terre ronde, de sorte que la Terre ne pourrait pas conserver son atmosphère. Y a-t-il peut-être un dôme transparent au-dessus de la Terre, qui empêche l'air de s'échapper ?

Dans le modèle traditionnel de la Terre plate, le Soleil est positionné au-dessus du disque, tournant dans le ciel comme un mobile pour bébés et à une distance beaucoup plus proche de la distance réelle. Le modèle n'explique pas les couchers et les levers de soleil. Pour un peu de bon sens, imaginons que le disque tourne comme une pièce de monnaie par rapport au Soleil. Cela permettrait au moins de retrouver le lever et le coucher de soleil. Même les animaux sont conscients de ce phénomène. Cependant, il n'y aurait plus de fuseaux horaires, car le lever et le coucher du soleil se feraient à la même heure partout dans le monde.

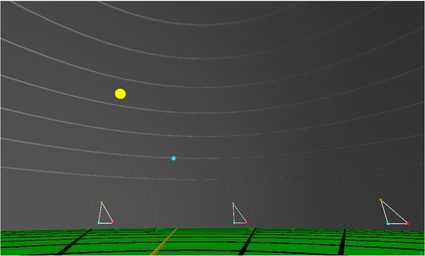
C'est le principal problème du modèle de la Terre plate. Il est plein d'incohérences et d'observations inexpliquées. Par exemple, pourquoi fait-il froid à la fois au centre et au bord du disque ?

Revenons à un mode de pensée plus scientifique et présentons la première expérience.

Cette première expérience peut être très simple à réaliser. Déplacez-vous vers le haut assez rapidement pour devancer l'ombre projetée par l'horizon. Vous pourrez alors voir une partie du coucher de soleil deux fois ! Cela veut dire que la Terre est bien ronde. Ce calculateur vous permet de calculer la quantité de temps dont vous pouvez « prolonger » le coucher de soleil, ainsi que la proportion du phénomène que vous verrez deux fois.

Que verriez-vous si la Terre était plate ? Pas de double coucher de soleil 😭. Quelle que soit la hauteur ou la vitesse à laquelle vous vous élevez depuis la surface d'une Terre plate, vous ne verriez plus le Soleil jusqu'à l'aube.

Imaginez l'ombre projetée par l'horizon terrestre qui vient vers vous et remonte le long de votre corps lorsque le Soleil se couche. Si vous parvenez à devancer cette ombre en vous déplaçant suffisamment vite vers le haut, vous pourrez à nouveau voir le coucher de soleil. Jetons un coup d'œil aux calculs.

Voilà l'équation qui relie le temps à la hauteur de l'ombre :

t = 8 × √h

où :

h – la hauteur de l'ombre
t – le temps que l'ombre met pour s'élever de h

Nous pouvons relier h à la différence entre la hauteur de départ et la hauteur finale, et t au temps qu'il faut pour se déplacer vers le haut. Comme nous ne pouvons pas passer d'une hauteur à l'autre instantanément, nous devons tenir compte du temps de déplacement. Enfin, pour déterminer la proportion du deuxième coucher de soleil que nous pourrons voir à nouveau, nous devons connaître la durée du coucher de soleil :

proportion du deuxième coucher de soleil = 100 × (1 - ((durée du coucher de soleil - t - temps de déplacement) / durée totale du double coucher de soleil))

Il existe plusieurs façons de revoir le Soleil juste après son coucher, de points de vue différents. Le calculateur Terre plate vs Terre ronde d'Omni vous permettra de savoir la quantité de temps dont vous pourrez « prolonger » le coucher de soleil. Voyons les trois idées qui nous viennent à l'esprit. 

1. Allongez-vous et levez-vous.

Cette idée est la plus simple en termes d'équipement. Vous avez juste besoin d'un endroit où vous pouvez voir le Soleil se coucher dans la mer ou sur un terrain complètement plat, tel qu'un désert. Un beau ciel sans nuages rendrait l'expérience encore meilleure. Il ne vous reste plus qu'à vous allonger et à regarder le coucher de soleil. Une fois que vous ne voyez plus le Soleil, levez-vous aussi vite que possible. Voilà le Soleil réapparaîtra !

Voici comment utiliser cet outil pour effectuer les calculs.

1. Sélectionnez un lieu proche de chez vous ou saisissez la durée du coucher de soleil à l'endroit où vous vous trouvez.
2. Saisissez la hauteur de départ : il s'agit du niveau de votre point de vue lorsque vous êtes allongé·e. Nous recommandons une hauteur d'environ 20 cm.
3. Indiquez le temps qu'il vous faudra pour vous lever. Nous estimons qu'il faut environ une demi-seconde, mais n'hésitez pas à vous chronométrer pour vérifier.
4. Entrez la hauteur finale, c'est-à-dire la hauteur à laquelle se trouvent vos yeux lorsque vous êtes debout. Vous pouvez mesurer cette hauteur en soustrayant de votre taille la distance entre le sommet de votre tête et vos yeux.
5. Le calculateur vous dira la proportion du coucher de soleil que vous pourrez voir à nouveau. Cette méthode devrait vous permettre de voir approximativement 5 % du deuxième coucher de soleil.

N'est-ce pas assez ? Essayez de modifier les valeurs dans le calculateur ou passez aux variantes plus avancées de l'expérience. Vous les trouverez ci-dessous.

2. Prenez l'ascenseur jusqu'en haut d'un gratte-ciel.

Pour voir une plus grande partie du deuxième coucher de soleil, vous devrez aller plus haut et plus vite pour devancer l'ombre de l'horizon. Pour ce faire, prenez un gratte-ciel doté d'un ascenseur rapide. Ce phénomène peut être observé grâce aux ascenseurs de l'hôtel Burj Khalifa, à Dubaï.

Pour calculer les détails de cette expérience un peu plus extrême, sélectionnez « Burj Khalifa : ascenseur vers le ciel » dans la liste déroulante. Si vous souhaitez essayer cette méthode sur un autre bâtiment, modifiez les valeurs selon vos besoins.

Cette expérience est pour vous si vous aimez les couchers de soleil, car elle vous permet de presque doubler la durée du coucher de soleil. En effet, vous devriez être en mesure de voir à nouveau 88 % du coucher de soleil.

3. Faites voler un drone.

Une autre idée consiste à utiliser un drone de bonne qualité équipé d'une caméra de transmission d'images en direct. Nous avons trouvé un drone qui peut atteindre 1 000 m en 200 secondes. Selon l'option « Drone » du calculateur, cette méthode vous permettra de revoir un tiers du coucher de soleil.

N'oubliez pas de vérifier la vitesse et la hauteur de votre drone et d'ajuster les valeurs dans le calculateur.

Dans cette expérience, nous allons cacher une partie d'un objet derrière la courbure de la Terre. Vous devrez trouver un plan d'eau dont la rive la plus éloignée se trouve au moins à 2 km. De plus, il faut que la journée soit calme et qu'il n'y ait pas de vent.

En outre, pour éviter l'effet de mirage (réfraction de lumière), réalisez l'expérience le matin, lorsqu'il fait frais. Nous déconseillons donc de le faire dans le désert : l'effet de mirage vous empêchera de voir suffisamment clair les objets situés sur la rive opposée.

Dans cette vidéo YouTube, un homme a fait disparaître un camion situé sur la rive opposée d'un lac à 7 km de lui en rapprochant sa caméra du sol.

Vous pouvez obtenir le même résultat lorsque vous observez des éoliennes :

Remarquez que plus l'éolienne est éloignée, plus elle est cachée. Le but de cette expérience est donc de calculer la part d'un objet éloigné que vous pouvez dissimuler derrière la courbure de la Terre.

Dans cette expérience, nous partirons d'un point de vue à une hauteur donnée, et nous descendrons ensuite vers le bas pour dissimuler un objet éloigné. En termes mathématiques, nous déterminerons la différence entre les parties cachées au départ et à la fin de l'expérience.

Pour calculer la partie cachée, nous devons d'abord connaître la distance entre nous et l'horizon. Cette distance est donnée par l'équation suivante :

a = √[(r + h)² - r²]

où :

• a – la distance à l'horizon
• h – le niveau du point de vue par rapport au sol
• r – le rayon de la Terre, égal à 6 371 km (3 959 miles)

Nous introduisons ensuite le résultat dans une deuxième équation qui calcule la partie de l'objet qui est masquée, x, si l'on observe l'objet à partir d'une hauteur nulle :

x = √(a² - 2ad + d² + r²) - r

La différence entre les deux valeurs de x est la hauteur de l'objet que nous pouvons faire disparaître en changeant notre point de vue.

Supposons que vous ayez trouvé un endroit idéal, par exemple un lac dont la rive se trouve à quelques kilomètres. Pour voir les objets situés sur la rive éloignée, vous aurez besoin de bonnes jumelles. C'est encore mieux si vous avez une caméra vidéo avec un zoom puissant. Cela vous permettra également d'enregistrer l'expérience, comme dans la vidéo ci-dessus.

Pour obtenir une vue stable à travers vos jumelles ou votre caméra, il est recommandé de les monter sur un trépied. L'utilisation d'un trépied vous permettra par ailleurs de mesurer les deux hauteurs avec précision.

Voici comment utiliser notre calculateur pour déterminer la partie de l'objet que vous pourriez faire disparaître derrière la courbure de la Terre.

1. Mesurez la distance jusqu'à la rive opposée du lac. Pour ce faire, vous pouvez utiliser une carte géographique traditionnelle ou la fonction de mesure de distance de Google Maps. Entrez cette distance dans le champ « Distance de l'objet ».
2. Mesurez la hauteur à laquelle se trouvent vos yeux lorsque vous êtes debout, ou la hauteur de votre appareil photo dans sa position de départ. Saisissez cette hauteur dans le deuxième champ.
3. Allongez-vous et mesurez la hauteur de vos yeux par rapport au sol, ou mesurez à quelle hauteur se trouve votre appareil photo dans sa position finale. Ensuite, saisissez cette mesure dans le dernier champ. Essayez de vous placer le plus bas possible par rapport au niveau de l'eau pour le meilleur effet.
4. Le calculateur effectuera tous les calculs. Vous verrez apparaître la hauteur de l'objet qui se cachera derrière l'horizon. Si vous n'arrivez pas à voir la différence entre vos vues en position de départ et en position finale, essayez de varier celles-ci.

Si la Terre était plate, vous ne verriez aucune différence, quelle que soit la hauteur à laquelle vous observez l'objet en question.

Cette expérience prouve non seulement que la Terre est ronde, mais elle permet aussi d'en estimer la circonférence. C'est exactement ce qu'a fait le mathématicien grec Ératosthène à Alexandrie vers 240 avant J.-C. Il savait qu'à Assouan, à environ 840 km (500 miles) au sud, il y avait un puits. La lumière du Soleil atteignait le fond de ce puits à midi lors du solstice d'été. Il a donc mesuré l'ombre portée d'un bâton à Alexandrie, ce qui l'a amené à conclure que la circonférence de la Terre était plus ou moins égale à 50 fois la distance entre Alexandrie et Assouan. Il est arrivé à cette conclusion par calculs mathématiques, en prenant en compte que la Terre était ronde et que le Soleil était très éloigné d'elle. Aujourd'hui, nous savons qu'il s'est trompé de moins de 10 %, ce qui est incroyable, étant donné que son expérience a eu lieu il y a 2 000 ans !

Comme vous pouvez le voir, le bâton et son ombre forment un triangle. Par conséquent, nous pouvons utiliser l'inverse de la fonction tangente pour calculer l'angle entre le bâton et la direction de la lumière, à l'aide de l'équation suivante :

θ = arctan(longueur de l'ombre / hauteur du bâton)

Nous devons effectuer ce calcul pour les deux bâtons. Comment ces deux angles se rapportent-ils à la circonférence de la Terre ? La figure ci-dessous nous aidera à répondre à cette question.

En utilisant un peu de géométrie, nous pouvons déterminer que la différence entre les angles des ombres est égale à α, c'est-à-dire l'angle entre les points A et B par rapport au centre de la Terre :

α = θ₂ - θ₁

Nous connaissons maintenant l'angle α et la longueur de l'arc (distance mesurée sur la surface de la Terre) entre A et B. Cela nous permet de calculer la circonférence totale à l'aide de proportions :

circonférence terrestre = distance A → B × (360° / α)

Il est important de noter que cette expérience fonctionne uniquement si le point A est situé directement au sud du point B (ou vice versa), car c'est le seul cas où les ombres des deux bâtons seront différentes.

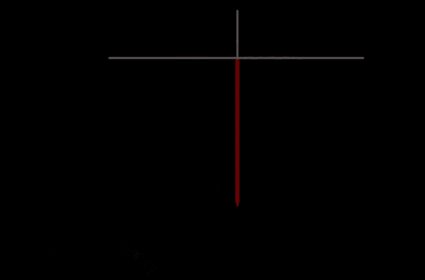
En supposant que le point A se trouve au sud du point B, tracez sur une carte une ligne vers le nord à partir du point A. Tracez ensuite une ligne vers l'est à partir du point B. La distance entre le point A et le point de rencontre entre les deux lignes est la distance verticale entre A et B.

Vous pouvez réaliser cette expérience de deux manières. Vous pouvez soit parcourir une distance considérable vers le nord ou le sud (plus de 160 km, mais plus c'est loin, mieux c'est), soit vous mettre d'accord avec quelqu'un qui vit à une latitude différente pour rendre l'expérience plus facile.

Commençons par la première option. Il est préférable de mener l'expérience le jour le plus court ou le plus long de l'année, car la durée du jour est relativement stable. Vous réduirez ainsi les erreurs qui pourraient se glisser dans les mesures des angles. Voici les instructions étape par étape :

1. Mesurez la hauteur de votre bâton et saisissez-la dans le premier champ du calculateur. Si une partie du bâton est dans le sol, n'indiquez que la hauteur au-dessus du sol.
2. Mesurez la longueur de l'ombre à l'endroit A à midi de l'heure locale. S'il n'a pas de Soleil, vous devrez reporter l'expérience à un autre jour. Entrez la longueur de l'ombre dans le calculateur. La mesure de l'angle apparaîtra automatiquement.
3. Rendez-vous à votre point B et procédez de la même manière qu'à l'étape 2.
4. À l'aide d'une carte géographique, mesurez la distance verticale (du nord au sud) entre les deux endroits et entrez ce chiffre dans le calculateur (voir les instructions ci-dessus).
5. Le calculateur estimera alors la circonférence de la Terre à partir de vos données. De cette manière, vous pourrez voir si votre réponse est proche de la circonférence réelle.

Si vous avez un ami qui se trouve à un autre endroit pour vous aider, c'est encore mieux ! L'expérience sera la plus précise si vous effectuez les deux mesures le même jour de l'année et à la même heure solaire. Dans ce cas, les étapes sont essentiellement les mêmes. Assurez-vous que les deux bâtons sont de la même longueur et que vous mesurez l'ombre à midi, heure locale, le même jour. Cette option est beaucoup plus facile et peut être réalisée n'importe quel jour ensoleillé de l'année.

Prenons l'exemple d'un voyage de la Floride à la Pennsylvanie (A à B), soit une distance d'environ 1 609 km (1 000 miles). Le bâton mesure 91 cm (3 pieds) de long, et il projette une ombre de 91 cm (3 pieds) en A. Cela signifie que l'ombre forme un angle de 45°. Nous nous rendons ensuite à notre point B, où notre ombre est de 157,8 cm (5,2 pieds). L'angle de l'ombre est donc d'environ 60°.

Saisissons nos données dans le calculateur. Selon nos estimations, la circonférence de la Terre est égale à 38 542 km (23 949 mi). Une erreur de 4 % s'est glissée : la circonférence réelle mesurée en passant par les pôles est de 40 008 km (24 860 mi).

Imaginons un instant que les partisans de la Terre plate aient raison. Comment l'exemple ci-dessus fonctionne-t-il dans un modèle de Terre plate ?

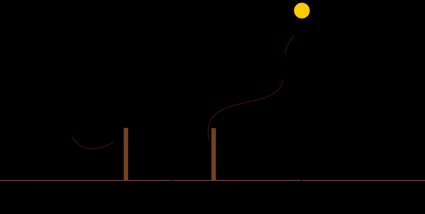
Dans un modèle de Terre plate, les ombres projetées par les bâtons seraient de différentes longueurs, comme c'est le cas en réalité. Cependant, les calculs de trigonométrie conduisent à un résultat étrange. En effectuant les calculs avec le diagramme ci-dessus comme référence, nous pouvons dire que :

d = h × (tan θ₂ - tan θ₁)

En résolvant l'équation pour les angles 45° et 60°, et 1 609 km, nous constatons que la distance au Soleil h est de :

h = 1 609 / (1,73 - 1) = 1 464 km

Cela peut sembler très proche de la réalité. Cependant, selon le modèle de la Terre plate, le Soleil est beaucoup plus petit que ce que la science a conclu jusqu'ici.

Nous pouvons maintenant calculer les distances entre nos deux points et le Soleil :

R₁ = h / cos θ₁ = 1 464 / cos(45°) = 2 070 km

R₂ = h / cos θ₂ = 1 464 / cos(60°) = 3 328 km

Cela signifierait qu'à cause d'un voyage de 1 609 km vers le sud, le Soleil perdrait 40 % de sa masse. Mais comme vous le savez, le Soleil ne devient pas plus petit quand un humain se déplace.

Nous pouvons donc conclure que le modèle de la Terre plate est erroné. Il ne correspond pas aux observations réelles. La propriété essentielle de tout modèle scientifique, c'est qu'il doit mener au même résultat que les expériences dans le monde réel.

L'idée que la Terre est sphérique est assez ancienne. En Grèce antique, les scientifiques et les philosophes étaient conscients de ce fait dès le V^e siècle avant J.-C.

Même au cours des siècles suivants, le modèle sphérique était plus largement accepté et n'était que marginalement remis en question : le seul champ qui rejetait cette théorie était la mythologie. La résurgence et la pertinence de la théorie de la Terre ronde à l'époque moderne n'est qu'une conséquence de l'évolution de nos méthodes de communication.

Pour calculer la circonférence de la Terre à l'aide d'ombres, suivez ces étapes :

1. Mettez un bâton dans le sol et mesurez sa hauteur.

2. Demandez à un ami vivant à une latitude différente de faire de même. Les deux bâtons doivent être de la même hauteur.

3. Mesurez l'angle entre les bâtons et la direction des rayons de soleil à la même heure de l'heure locale à l'aide de la formule suivante :
   θ = arctan(longueur de l'ombre / hauteur du bâton)

4. Utilisez maintenant la formule de la circonférence de la Terre :
   circonférence de la Terre = d × (360° / α)

   où :

   • d – la distance entre les latitudes auxquelles sont situés les bâtons
   • α – la différence entre les angles calculés précédemment

Pour voir la courbure de la Terre, vous devez vous trouver à une altitude d'environ 10,5 km (35 000 pieds). C'est à peu près l'altitude de croisière d'un avion de ligne. Cependant, pour le voir bien, le ciel doit être dégagé, sans aucun nuage, et vous devez disposer d'un champ de vision d'au moins 60 degrés. Lors d'un voyage en avion, ces deux conditions sont rarement remplies, mais rien ne vous empêche d'essayer.

Comme vous l'aurez peut-être remarqué, la courbure de la Terre n'est pas visible même depuis le sommet du mont Everest !

Pour prouver que la Terre est ronde, allez à la plage ! Si vous voyez bien l'horizon, vous n'avez qu'à attendre qu'un navire se rapproche de la côte. Petit à petit, vous verrez la partie supérieure du navire apparaître, et le reste suivra.
Cela est dû à la courbure de la Terre : l'horizon révèle le navire au fur et à mesure qu'il vient vers vous.

Maintenant, le plus difficile est de convaincre les sceptiques !