Calculateur de fréquence

Le calculateur de fréquence vous permettra de trouver la fréquence d'une onde donnée en fonction de sa période ou de sa longueur d'onde et de sa vitesse en un rien de temps. Vous pouvez choisir une vitesse d'onde dans la liste prédéfinie, ce qui vous évite d'avoir à vous en souvenir.

Dans ce texte, vous trouverez également la définition de la fréquence, deux formules de fréquence (l'une en fonction de la longueur d'onde et l'autre en fonction de la période), ainsi que quelques exemples montrant comment calculer la fréquence.

Si vous voulez en savoir plus sur les ondes, consultez notre calculateur de longueur d'onde, et si vous voulez connaître la fréquence des notes de musique, consultez le calculateur de fréquence des notes 🇺🇸.

Observez le modèle d'onde suivant ; il vous aidera à comprendre les termes utilisés dans la définition de la fréquence qui se trouve en dessous.

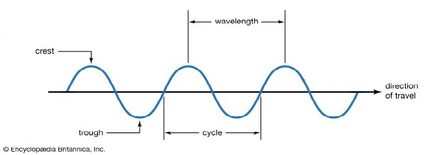
La fréquence est le nombre d'oscillations (cycles) réalisé par seconde. En d'autres termes, la fréquence nous indique combien de crêtes d'onde passent par un point donné en une seconde.

Cette définition de la fréquence nous conduit à la formule de fréquence la plus simple :

où :

$f$ – la fréquence
$T$ – le temps nécessaire pour accomplir une oscillation, mesuré en secondes

L'unité SI de la fréquence est le hertz (Hz), qui équivaut à 1/s (une oscillation par seconde). Les autres unités de fréquence sont le millihertz (mHz), le kilohertz (kHz), le mégahertz (MHz), le gigahertz (GHz) et le térahertz (THz).

Jetez un coup d'œil à cette autre image qui vous permettra de mieux comprendre la relation entre la fréquence et la longueur d'onde. La longueur d'onde est la distance entre deux crêtes adjacentes (ou creux). En d'autres termes, c'est la longueur d'oscillation. Plus la longueur d'onde est grande, plus la fréquence est basse :

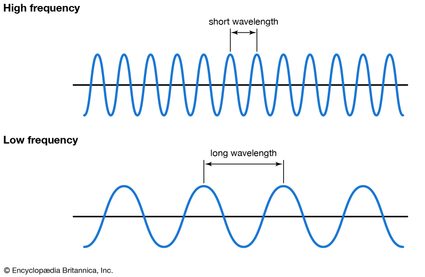
Autre donnée nécessaire : la vitesse de déplacement des ondes détermine le nombre d'ondes qui passeront par un point donné en une seconde. En d'autres termes, plus la vitesse de l'onde est élevée, plus la fréquence est élevée.

Ces deux relations entre la fréquence et la longueur d'onde $(\lambda)$ et entre la fréquence et la vitesse ($v$) nous amènent à l'équation de fréquence suivante :

Notre calculateur de fréquence intègre les formules de fréquence mentionnées précédemment. Vous pouvez donc l'utiliser comme calculateur de fréquence en fonction de la période ou comme calculateur de fréquence en fonction de la longueur d'onde.

Comment l'utiliser comme calculateur de fréquence par rapport à la période ? (Comment trouver la fréquence si vous connaissez la période ?)

1. Entrez la durée d'une oscillation (période). Le calculateur déterminera la fréquence.

2. Vous pouvez utiliser ce calculateur pour déterminer la période si vous connaissez sa fréquence.

Comment l'utiliser comme calculateur de fréquence par rapport à la longueur d'onde ? (Comment calculer la fréquence si vous connaissez la longueur d'onde ?)

1. Choisissez le type d'onde et son milieu dans la liste déroulante du premier champ. Par défaut, il s'agit de lumière dans le vide. Si vous sélectionnez l'option « Vitesse d'onde personnalisée », vous pouvez saisir une vitesse d'onde de votre choix.

2. Entrez la longueur d'onde et la valeur de la fréquence apparaîtra.

En fait, vous pouvez entrer deux variables quelconques et la troisième apparaîtra immédiatement ! 😀

Pour dissiper tout doute sur la manière de calculer la fréquence à partir de la période, analysons quelques exemples simples. Tout d'abord, rappelez-vous l'équation de la fréquence :

Premier exemple

Comment trouver la fréquence d'une onde dont la durée d'oscillation est de 0,25 s ?

N'oubliez pas de convertir $\frac{1}{\text{s}}$ en unité de fréquence :

Deuxième exemple

Comment trouver la fréquence d'une onde dans laquelle 360 oscillations se produisent en 1 minute ?

Cette fois-ci, nous voulons savoir comment trouver la fréquence d'une onde si vous connaissez la vitesse de l'onde et la longueur d'onde. Vous devez utiliser la formule de fréquence suivante :

Premier exemple

La vitesse d'une onde est égale à 320 m/s, et sa longueur d'onde est de 8 m. Pour trouver sa fréquence, nous arrivons à :

Deuxième exemple

Trouvez la fréquence de la lumière si la longueur d'onde est égale à 3 000 km. La vitesse de l'onde est alors égale à la vitesse de la lumière dans le vide, qui est d'environ $300\, 000\ \tfrac{\text{km}}{\text{s}}$. En utilisant la formule de la fréquence, nous obtenons :

Dans les communications sans fil, nous avons un volume ellipsoïde entre l'antenne émettrice et l'antenne réceptrice. Cette région est déterminée par la distance entre les antennes et la fréquence de l'onde sans fil. Elle est appelée zone de Fresnel et se présente comme ceci :

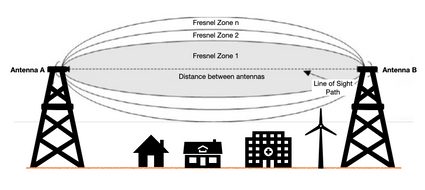
Nous déduisons de la formule principale de la zone de Fresnel que plus la fréquence est élevée, plus le volume de l'ellipsoïde nécessaire pour une communication sans fil adéquate est petit. À l'inverse, pour une fréquence faible, nous obtenons une zone de Fresnel plus grande que la présence de bâtiments ou d'arbres peuvent facilement bloquer et, par conséquent, produire une communication sans fil instable.

Lorsque deux ondes de fréquences différentes interfèrent l'une avec l'autre de manière constructive et destructive, elles produisent un modèle d'interaction appelé battement. Vous pouvez trouver la fréquence spécifique d'un battement à l'aide du calculateur de fréquence de battement 🇺🇸 d'Omni.

Un autre phénomène intéressant dû à l'interaction d'ondes de différentes fréquences est la résonance. La résonance peut se produire, par exemple, lorsque de l'air traverse une cavité, comme quand on souffle sur le goulot d'une bouteille vide.

Cette cavité résonnante est appelée résonateur de Helmholtz. Si le volume de la cavité change, la fréquence de résonance change. Vous pouvez déterminer la fréquence de résonance de cavités de différents volumes à l'aide de notre calculateur de résonateur de Helmholtz 🇺🇸.