Calculadora de ángulos de un triángulo

La calculadora de ángulos de un triángulo es la mejor opción si deseas aprender cómo determinar los ángulos de un triángulo. Tanto si tienes dados tres lados de un triángulo, dos lados y un ángulo o solo dos ángulos, esta herramienta es la solución a tus problemas de geometría. A continuación también encontrarás la explicación de las leyes fundamentales relativas a los ángulos de un triángulo: el teorema de la suma de los ángulos internos de un triángulo, el teorema del ángulo exterior de un triángulo y el teorema de la bisectriz de un ángulo. Sigue leyendo para aprender cómo funciona la calculadora y pruébala: ¡encontrar los ángulos que faltan en los triángulos nunca ha sido tan fácil!

Hay varias formas de hallar los ángulos de un triángulo, dependiendo de los datos que se den:

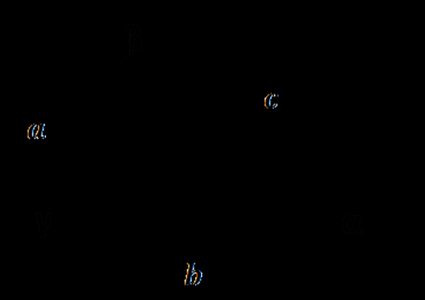
1. Dados tres lados del triángulo

Utiliza las fórmulas transformadas de la ley del coseno:

Entonces:

Para el segundo ángulo tenemos:

Entonces:

Y finalmente, para el tercer ángulo:

Entonces:

2. Dados dos lados del triángulo y un ángulo

Si el ángulo está entre los dos lados conocidos, puedes utilizar directamente la ley del coseno para hallar el tercer lado desconocido. Luego, puedes aplicar las fórmulas previas para encontrar los ángulos restantes. Por ejemplo, si tienes los valores de a, b, y γ:

• calcula $c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$;
• sustituye $c$ por $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$;
• luego halla $\beta$ a partir del teorema de la suma de ángulos del triángulo: $\beta = 180\degree- \alpha - \gamma$

Si el ángulo no está entre los lados conocidos, puedes recurrir a la ley de los senos. Por ejemplo, supongamos que conocemos $a$, $b$, y $\alpha$:

Entonces:

• Como sabes, la suma de los ángulos internos de un triángulo es igual a $180\degree$. A partir de este teorema podemos hallar el ángulo que falta como: $\gamma = 180\degree- \alpha - \beta$.

3. Dados dos ángulos

Es la opción más fácil. Basta con utilizar el teorema de la suma de ángulos internos de un triángulo para hallar el ángulo restante:

• $\alpha = 180\degree- \beta - \gamma$;
• $\beta= 180\degree- \alpha - \gamma$; y
• $\gamma = 180\degree- \alpha- \beta$

En los tres casos, puedes utilizar nuestra calculadora de ángulos de un triángulo, no te defraudará.

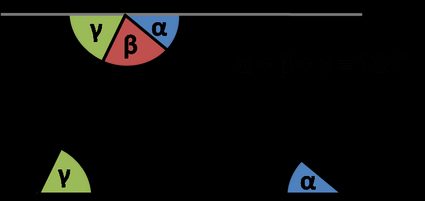
El teorema afirma que los ángulos internos de un triángulo suman $180\degree$:

¿Cómo lo sabemos? Observa la imagen: los ángulos marcados con las mismas letras griegas son congruentes porque son ángulos internos alternos. La suma de los tres ángulos $\alpha$ $\beta$ , $\gamma$ es igual a $180\degree$, ya que forman una línea recta. Sin embargo, estos son tres ángulos interiores de un triángulo, lo que nos lleva a la ecuación $\alpha + \beta+ \gamma = 180\degree$.

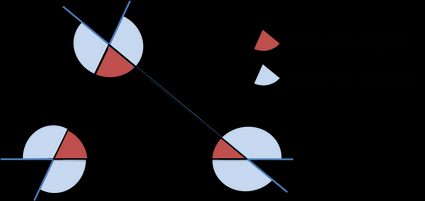
Un ángulo exterior de un triángulo es igual a la suma de los ángulos internos opuestos.

• Cada triángulo consta de seis ángulos exteriores (dos en cada vértice que tienen la misma medida).
• La suma de los ángulos exteriores, tomando uno de cada vértice, siempre es igual a $360\degree$.
• Un ángulo exterior es suplementario a su ángulo interior del triángulo adyacente.

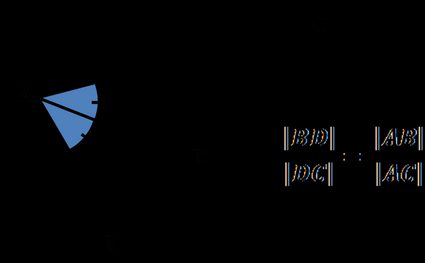
El teorema de la bisectriz del ángulo establece que:

La bisectriz de un ángulo de un triángulo divide el lado opuesto en dos segmentos proporcionales a los otros dos lados del triángulo.

En otras palabras:

La relación entre la longitud de $\overline{BD}$ y la longitud de $\overline{DC}$ es igual a la relación entre la longitud del lado $\overline{AB}$ y la longitud del lado $\overline{AC}$:

Bien, practiquemos lo que acabamos de aprender. Supongamos que queremos encontrar los ángulos que faltan en nuestro triángulo. ¿Cómo lo hacemos?

1. Averigua qué fórmulas necesitas utilizar. En nuestro ejemplo, tenemos dos lados y un ángulo. Elige la opción ángulo y 2 lados.
2. Ingresa los valores. Por ejemplo, sabemos que $a = 9\ \mathrm{cm}$, $b = 14\ \mathrm{cm}$, y $\alpha = 30\degree$. Si quieres calcularlo manualmente, utiliza la ley de los senos:

Entonces:

• A partir de lo que sabemos sobre la suma ángulos internos en un triángulo, calculamos que $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51.06\degree= 98.94\degree$.

3. La calculadora de ángulos de un triángulo encuentra los ángulos que faltan en el triángulo. Son iguales a los que calculamos manualmente:$\beta = 51.06\degree$, $\gamma = 98.94\degree$; además, la herramienta determinó la longitud del último lado: $c = 17.78\ \mathrm{cm}$.

Un razonamiento similar al que aplicamos en esta calculadora aparece en otros cálculos de triángulos, ¡por ejemplo los que utilizamos en la calculadora de triángulos ALA 🇺🇸 y en la calculadora de triángulos LLA 🇺🇸!